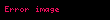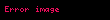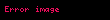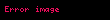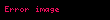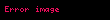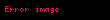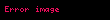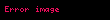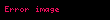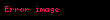Matematikte Hadwiger–Finsler eşitsizliği, Öklid düzlemindeki üçgen geometrisinin bir sonucudur. Düzlemdeki bir üçgenin kenar uzunlukları , ve ve alanı ile gösterilirse, o zaman
İlgili eşitsizlikler
- , Hadwiger–Finsler eşitsizliğinin doğrudan bir : düzlemdeki bir üçgenin kenar uzunlukları
,
ve
ve alanı
ile gösterilirse, o zaman
Weitzenböck eşitsizliği, Heron formülü kullanılarak da kanıtlanabilir; bu yolla, (W) için eşitliğin ancak ve ancak eğer üçgen bir eşkenar üçgen ise, yani 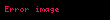
- Dörtgen için bir versiyon:
, uzunlukları
,
,
,
ve alanı
ile gösterilen dışbükey bir dörtgen olsun, sonra:
sadece bir kare için eşitlikle sonuçlanır.
Burada; 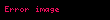
İspat
Kosinüs yasasından aşağıdaki ifadeyi elde ederiz:




'dir.
ve
olduğunu hatırlarsak, bunları kullanarak aşağıdaki ifadeyi elde edebiliriz;
Bunu üçgenin her kenarı için yaparak ve taraf tarafa toplayarak aşağıdaki ifadeyi elde ederiz:


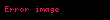

Bunu kullanarak aşağıdaki ifadeyi elde ederiz:
Bu da Hadwiger–Finsler eşitsizliğidir.
Tarihçe
Hadwiger–Finsler eşitsizliğine, Alman ve İsviçreli matematikçi ile İsviçreli matematikçi yaptıkları çalışma ( & 1937) sonrası adını vermiştir, aynı makalede, bir tepe noktasını paylaşan diğer iki kareden türetilen bir kare üzerinde Finsler–Hadwiger teoremini de yayınladılar.
Eşitsizliğin genelleştirilmesi
1. Eğer 




'dir.
Eşitlik ancak ve ancak dörtgen bir kare ise doğrudur.
2. Eğer 
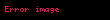
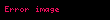

……
'dir.
Eşitlik, ancak ve ancak n-kenarlı şekil eş kenarlı bir n-kenarlı şekil ise doğrudur.
Ayrıca bakınız
Notlar
- ^ Leonard Mihai Giugiuc, Dao Thanh Oai and Kadir Altintas, An inequality related to the lengths and area of a convex quadrilateral, International Journal of Geometry, Vol. 7 (2018), No. 1, ss. 81-86
Kaynakça
- ; (1937). "Einige Relationen im Dreieck". . 10 (1): 316-326. doi:10.1007/BF01214300.
- Claudi Alsina, Roger B. Nelsen: When Less is More: Visualizing Basic Inequalities. MAA, 2009, , pp. 84-86 21 Temmuz 2018 tarihinde Wayback Machine sitesinde .
Dış bağlantılar
- PlanetMath'te Proof of Hadwiger-Finsler inequality
- PlanetMath'te Weizenbock's inequality
Konuyla ilgili yayınlar
- Cezar Lupu (27 Ocak 2010), Algebraic-Geometric Proofs of the Weitzenbock and Finsler-Hadwiger Inequalities Revisited (PDF)
- D. Ş. Marinescu; M. Monea; M. Opincariu; M. Stroe (2012), "Note on Hadwinger–Finsler's Inequalites" (PDF), Journal of Mathematical Inequalities, 6 (1), ss. 57-64, 9 Ağustos 2017 tarihinde kaynağından (PDF), erişim tarihi: 6 Aralık 2020
- Kouba, Omran (2017), "On certain new refinements of Finsler-Hadwiger inequalities", Journal of Inequalities and Applications, doi:10.1186/s13660-017-1356-5
wikipedia, wiki, viki, vikipedia, oku, kitap, kütüphane, kütübhane, ara, ara bul, bul, herşey, ne arasanız burada,hikayeler, makale, kitaplar, öğren, wiki, bilgi, tarih, yukle, izle, telefon için, turk, türk, türkçe, turkce, nasıl yapılır, ne demek, nasıl, yapmak, yapılır, indir, ücretsiz, ücretsiz indir, bedava, bedava indir, mp3, video, mp4, 3gp, jpg, jpeg, gif, png, resim, müzik, şarkı, film, film, oyun, oyunlar, mobil, cep telefonu, telefon, android, ios, apple, samsung, iphone, xiomi, xiaomi, redmi, honor, oppo, nokia, sonya, mi, pc, web, computer, bilgisayar
Matematikte Hadwiger Finsler esitsizligi Oklid duzlemindeki ucgen geometrisinin bir sonucudur Duzlemdeki bir ucgenin kenar uzunluklari a displaystyle a b displaystyle b ve c displaystyle c ve alani T displaystyle T ile gosterilirse o zaman a2 b2 c2 a b 2 b c 2 c a 2 43T HF displaystyle a 2 b 2 c 2 geq a b 2 b c 2 c a 2 4 sqrt 3 T quad mbox HF Ilgili esitsizlikler Hadwiger Finsler esitsizliginin dogrudan bir duzlemdeki bir ucgenin kenar uzunluklari a displaystyle a b displaystyle b ve c displaystyle c ve alani T displaystyle T ile gosterilirse o zamana2 b2 c2 43T W displaystyle a 2 b 2 c 2 geq 4 sqrt 3 T quad mbox W Weitzenbock esitsizligi Heron formulu kullanilarak da kanitlanabilir bu yolla W icin esitligin ancak ve ancak eger ucgen bir eskenar ucgen ise yani a b c displaystyle a b c icin gecerli oldugu gorulur Dortgen icin bir versiyon ABCD displaystyle ABCD uzunluklari a displaystyle a b displaystyle b c displaystyle c d displaystyle d ve alani T displaystyle T ile gosterilen disbukey bir dortgen olsun sonra a2 b2 c2 d2 4T 3 13 a b 2 displaystyle a 2 b 2 c 2 d 2 geq 4T frac sqrt 3 1 sqrt 3 sum a b 2 sadece bir kare icin esitlikle sonuclanir Burada a b 2 a b 2 a c 2 a d 2 b c 2 b d 2 c d 2 displaystyle sum a b 2 a b 2 a c 2 a d 2 b c 2 b d 2 c d 2 IspatKosinus yasasindan asagidaki ifadeyi elde ederiz a2 b2 c2 2bccos a displaystyle a 2 b 2 c 2 2bc cos alpha a displaystyle alpha b displaystyle b ve c displaystyle c arasindaki aci olsun Bu asagidaki ifadeye donusturulebilir a2 b c 2 2bc 1 cos a displaystyle a 2 b c 2 2bc 1 cos alpha A 12bcsin a displaystyle A frac 1 2 bc sin alpha oldugundan a2 b c 2 4A1 cos asin a displaystyle a 2 b c 2 4A frac 1 cos alpha sin alpha dir 1 cos a 2sin2 a2 displaystyle 1 cos alpha 2 sin 2 frac alpha 2 ve sin a 2sin a2cos a2 displaystyle sin alpha 2 sin frac alpha 2 cos frac alpha 2 oldugunu hatirlarsak bunlari kullanarak asagidaki ifadeyi elde edebiliriz a2 b c 2 4Atan a2 displaystyle a 2 b c 2 4A tan frac alpha 2 Bunu ucgenin her kenari icin yaparak ve taraf tarafa toplayarak asagidaki ifadeyi elde ederiz a2 b2 c2 a b 2 b c 2 c a 2 4A tan a2 tan b2 tan g2 displaystyle a 2 b 2 c 2 a b 2 b c 2 c a 2 4A left tan frac alpha 2 tan frac beta 2 tan frac gamma 2 right b displaystyle beta ve g displaystyle gamma ucgenin diger acilaridir Simdi ucgenin acilarinin yarisi p2 displaystyle frac pi 2 den kucuk oldugundan tan displaystyle tan fonksiyonu disbukeydir tan a2 tan b2 tan g2 3tan a b g6 3tan p6 3 displaystyle tan frac alpha 2 tan frac beta 2 tan frac gamma 2 geq 3 tan frac alpha beta gamma 6 3 tan frac pi 6 sqrt 3 Bunu kullanarak asagidaki ifadeyi elde ederiz a2 b2 c2 a b 2 b c 2 c a 2 4A3 displaystyle a 2 b 2 c 2 geq a b 2 b c 2 c a 2 4A sqrt 3 Bu da Hadwiger Finsler esitsizligidir TarihceHadwiger Finsler esitsizligine Alman ve Isvicreli matematikci ile Isvicreli matematikci yaptiklari calisma amp 1937 sonrasi adini vermistir ayni makalede bir tepe noktasini paylasan diger iki kareden turetilen bir kare uzerinde Finsler Hadwiger teoremini de yayinladilar Esitsizligin genellestirilmesi1 Eger a displaystyle a b displaystyle b c displaystyle c ve d displaystyle d bir dortgenin dort kenariysa ve S displaystyle S alani ise o zaman a2 b2 c2 d2 4S displaystyle a 2 b 2 c 2 d 2 geq 4S dir Esitlik ancak ve ancak dortgen bir kare ise dogrudur 2 Eger L1 displaystyle L 1 L2 displaystyle L 2 Ln displaystyle L n n kenarli seklin kenar uzunluklari ve S displaystyle S alani ise o zaman L12 L22 displaystyle L 1 2 L 2 2 Ln2 4Stan pn n 3 displaystyle L n 2 geq 4S tan tfrac pi n n geq 3 dir Esitlik ancak ve ancak n kenarli sekil es kenarli bir n kenarli sekil ise dogrudur Ayrica bakinizNotlar Leonard Mihai Giugiuc Dao Thanh Oai and Kadir Altintas An inequality related to the lengths and area of a convex quadrilateral International Journal of Geometry Vol 7 2018 No 1 ss 81 86Kaynakca 1937 Einige Relationen im Dreieck 10 1 316 326 doi 10 1007 BF01214300 Claudi Alsina Roger B Nelsen When Less is More Visualizing Basic Inequalities MAA 2009 9780883853429 pp 84 86 21 Temmuz 2018 tarihinde Wayback Machine sitesinde Dis baglantilarPlanetMath te Proof of Hadwiger Finsler inequality PlanetMath te Weizenbock s inequalityKonuyla ilgili yayinlarCezar Lupu 27 Ocak 2010 Algebraic Geometric Proofs of the Weitzenbock and Finsler Hadwiger Inequalities Revisited PDF D S Marinescu M Monea M Opincariu M Stroe 2012 Note on Hadwinger Finsler s Inequalites PDF Journal of Mathematical Inequalities 6 1 ss 57 64 9 Agustos 2017 tarihinde kaynagindan PDF erisim tarihi 6 Aralik 2020 Kouba Omran 2017 On certain new refinements of Finsler Hadwiger inequalities Journal of Inequalities and Applications doi 10 1186 s13660 017 1356 5
 Azərbaycanca
Azərbaycanca Deutsch
Deutsch 日本語
日本語 Lietuvos
Lietuvos සිංහල
සිංහල Türkçe
Türkçe Українська
Українська United State
United State