Matematikte genişletilmiş gerçel sayı sistemi gerçel sayılar kümesi ile ve bileşimi olan kümedir. Bu küme, gerçel sayı sistemi ye her gerçel sayıdan büyük olan ve her gerçel sayıdan küçük olan 'un eklenmesiyle elde edilen sayı sistemidir. Böylelikle, artı sonsuza artan veya eksi sonsuza azalan dizilerin ya da anlamlı bir hâle getirilmiş olur. ve analizde, ve 'un gerçek limit olarak kullanılmasıyla hesaplamalar önemli ölçüde genişler. Genişletilmiş gerçel sayı sistemi gerçel sayıların .
Genişletilmiş gerçel sayı sistemi ile gösterilir. Kullanılan diğer gösterimler arasında ve gösterimleri de vardır. Hatta, kullanımının anlaşıldığı durumlarda bu gösterimin yerine sadece gösterimi de kullanılır.
Ayrıca, projektif genişletilmiş gerçel sayılar doğrusu da vardır. Bu sayı doğrusunda ve ayrıt edilmez ve hem sonsuza artan diziler hem de sonsuza azalan diziler için sadece ile gösterilen tek bir gerçek sonsuzluk vardır.
Kaynakça
- ^ Terimler.org sayfasında genişletilmiş gerçel sayılar sistemi teriminin tanımı. Erişim tarihi: 1 Şubat 2025.
- ^ Wilkins, David (2007). "Section 6: The Extended Real Number System" (PDF). maths.tcd.ie. 5 Ocak 2011 tarihinde kaynağından (PDF) arşivlendi. Erişim tarihi: 3 Aralık 2019.
- ^ Oden, J. Tinsley; Demkowicz, Leszek (16 Ocak 2018). Applied Functional Analysis. 3. Chapman and Hall/CRC. s. 74. ISBN . 8 Aralık 2019 tarihinde kaynağından arşivlendi. Erişim tarihi: 8 Aralık 2019.
 | Matematik ile ilgili bu madde seviyesindedir. Madde içeriğini genişleterek Vikipedi'ye katkı sağlayabilirsiniz. |
wikipedia, wiki, viki, vikipedia, oku, kitap, kütüphane, kütübhane, ara, ara bul, bul, herşey, ne arasanız burada,hikayeler, makale, kitaplar, öğren, wiki, bilgi, tarih, yukle, izle, telefon için, turk, türk, türkçe, turkce, nasıl yapılır, ne demek, nasıl, yapmak, yapılır, indir, ücretsiz, ücretsiz indir, bedava, bedava indir, mp3, video, mp4, 3gp, jpg, jpeg, gif, png, resim, müzik, şarkı, film, film, oyun, oyunlar, mobil, cep telefonu, telefon, android, ios, apple, samsung, iphone, xiomi, xiaomi, redmi, honor, oppo, nokia, sonya, mi, pc, web, computer, bilgisayar
Matematikte genisletilmis gercel sayi sistemi gercel sayilar kumesi ile ve bilesimi olan kumedir Bu kume gercel sayi sistemi R displaystyle mathbb R ye her gercel sayidan buyuk olan displaystyle infty ve her gercel sayidan kucuk olan displaystyle infty un eklenmesiyle elde edilen sayi sistemidir Boylelikle arti sonsuza artan veya eksi sonsuza azalan dizilerin ya da anlamli bir hale getirilmis olur ve analizde displaystyle infty ve displaystyle infty un gercek limit olarak kullanilmasiyla hesaplamalar onemli olcude genisler Genisletilmis gercel sayi sistemi gercel sayilarin Genisletilmis gercel sayi sistemi R displaystyle overline mathbb R ile gosterilir Kullanilan diger gosterimler arasinda displaystyle infty infty ve R displaystyle mathbb R cup left infty infty right gosterimleri de vardir Hatta displaystyle infty kullaniminin anlasildigi durumlarda bu gosterimin yerine sadece displaystyle infty gosterimi de kullanilir Ayrica projektif genisletilmis gercel sayilar dogrusu da vardir Bu sayi dogrusunda displaystyle infty ve displaystyle infty ayrit edilmez ve hem sonsuza artan diziler hem de sonsuza azalan diziler icin sadece displaystyle infty ile gosterilen tek bir gercek sonsuzluk vardir Kaynakca Terimler org sayfasinda genisletilmis gercel sayilar sistemi teriminin tanimi Erisim tarihi 1 Subat 2025 Wilkins David 2007 Section 6 The Extended Real Number System PDF maths tcd ie 5 Ocak 2011 tarihinde kaynagindan PDF arsivlendi Erisim tarihi 3 Aralik 2019 Oden J Tinsley Demkowicz Leszek 16 Ocak 2018 Applied Functional Analysis 3 Chapman and Hall CRC s 74 ISBN 9781498761147 8 Aralik 2019 tarihinde kaynagindan arsivlendi Erisim tarihi 8 Aralik 2019 Matematik ile ilgili bu madde taslak seviyesindedir Madde icerigini genisleterek Vikipedi ye katki saglayabilirsiniz
 Azərbaycanca
Azərbaycanca Deutsch
Deutsch 日本語
日本語 Lietuvos
Lietuvos සිංහල
සිංහල Türkçe
Türkçe Українська
Українська United State
United State

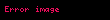

![{\displaystyle [-\infty ,+\infty ]}](https://www.wikipedia.tr-tr.nina.az/image/aHR0cHM6Ly93d3cud2lraXBlZGlhLnRyLXRyLm5pbmEuYXovaW1hZ2UvYUhSMGNITTZMeTkzYVd0cGJXVmthV0V1YjNKbkwyRndhUzl5WlhOMFgzWXhMMjFsWkdsaEwyMWhkR2d2Y21WdVpHVnlMM04yWnk5aE4yRTFZVFZpWVRRM09EazJaVGhtWkdRME0yTm1OMll6TVRGa1lqSTNNelV3WmpCbU9HWm0uc3Zn.svg)