Azərbaycanca AzərbaycancaDeutsch Deutsch日本語 日本語Lietuvos Lietuvosසිංහල සිංහලTürkçe TürkçeУкраїнська УкраїнськаUnited State United State
Destek
www.wikipedia.tr-tr.nina.az
  • Vikipedi

Kriptografide Eliptik Eğri Dijital imza Algoritması ECDSA eliptik eğri şifrelemesi kullanan birçok çeşit Dijital imza Al

Eliptik eğri dijital imza algoritması

Eliptik eğri dijital imza algoritması
www.wikipedia.tr-tr.nina.azhttps://www.wikipedia.tr-tr.nina.az
TikTok Jeton Satışı

Kriptografide Eliptik Eğri Dijital İmza Algoritması (ECDSA), eliptik eğri şifrelemesi kullanan birçok çeşit Dijital İmza Algoritması (DSA) sunar.

DSA ile anahtar ve imza boyut karşılaştırması

Genel olarak eliptik eğri kriptografisinde olduğu gibi, açık anahtarın bit boyutu ECDSA için yeterli olduğu düşünülen güvenlik seviyesinin bitlerin yaklaşık iki katı kadardır. Örneğin, 80 bitlik bir güvenlik düzeyinde bir ECDSA' nın (yani saldırganın gizli anahtarı bulmak için maksimum 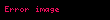280{\displaystyle 2^{80}}imageoperasyon deneme yapması gerektiği anlamına gelir) genel anahtarının boyutu 160 bit olurken, bir DSA genel anahtarının boyutu en az 1024 bit'tir. Öte yandan, güvenlik seviyesinin t{\displaystyle {t}}image uzunluğunda olduğu hem DSA hem de ECDSA için imza boyutu yaklaşık 4t{\displaystyle 4t}imageolur, başka bir deyişle 80 bit güvenlik düzeyi için yaklaşık 320 bitlik imza gerekir.

İmza oluşturma algoritması

Diyelim ki imzalı bir mesaj göndermek istiyor. İlk olarak, eğri parametreleri olan 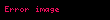(CURVE,G,n){\displaystyle {\displaystyle ({\textrm {CURVE}},G,n)}}imageüzerinde anlaşmalıdırlar. Cisme ve eğri eşitliğine ek olarak, eğri üzerinde asal mertebenin temel noktası olan G ve G' nin çarpımsal mertebesi olan n' ye ihtiyaç vardır.

Parametre
EĞRİ eliptik eğri alanı ve kullanılan denklem
G, eliptik eğri taban noktası, ör: 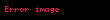y2=x3+7{\displaystyle y^{2}=x^{3}+7}image, n. mertebeden çok büyük bir asal ile eliptik eğri üreticisi.
n G' nin tam sayı mertebesi, yani 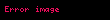nxG=O{\displaystyle nxG=O}image, burada O{\displaystyle O}imagetanımlayıcı elemandır.
dA Rastgele seçilmiş gizli anahtar
Qa Eliptik eğriden hesaplanmış açık anahtar
m mesaj

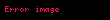
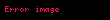
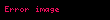
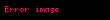
n{\displaystyle n}image asal bir sayı olmak zorundadır. Aslında, Z/nZ{\displaystyle \mathbb {Z} /n\mathbb {Z} }imagehalkasının sıfırdan farklı her elemanının tersine olduğunu varsayarız, yani Z/nZ{\displaystyle \mathbb {Z} /n\mathbb {Z} }image cisim olmak zorundadır. Buda bize n{\displaystyle n}image' nin asal olması gerektiğini gösterir. (bkn. Bézout Teoremi)

Alice, [1,n−1]{\displaystyle [1,n-1]}image aralığından rastgele seçilmiş özel anahtar olan dA{\displaystyle d_{A}}image 'yı ve eğrinin public keyi olan QA=dA×G{\displaystyle Q_{A}=d_{A}\times G}image içeren bir anahtar çifti oluşturur. ×{\displaystyle \times }image, eliptik eğri skaler nokta çarpımını temsil eder.

Alice, m{\displaystyle m}imagemesajını imzalayabilmesi için aşağıdaki adımları takip etmelidir:

  1. e=HASH(m){\displaystyle e=HASH(m)}image'yi hesaplar. (Burada HASH Kriptografik özet fonksiyonu temsil eder.)
  2. z{\displaystyle z}image, e{\displaystyle e}image 'in en solundaki bitleri olan Ln{\displaystyle L_{n}}image olsun; burada Ln{\displaystyle L_{n}}image n. mertebeden bir grubun mertebesi olsun.
  3. [1,n−1]{\displaystyle [1,n-1]}image arasından kriptografik olarak güvenli rastgele bir tam sayı k{\displaystyle k}image seçer.
  4. Eğri noktaları olan (x1,y1)=k×G{\displaystyle (x_{1},y_{1})=k\times G}image hesaplar.
  5. r=x1modn{\displaystyle r=x_{1}{\bmod {n}}}image hesaplanır. Eğer r=0{\displaystyle r=0}image ise 3. adıma geri dönülür.
  6. s=k−1(z+rdA)modn{\displaystyle s=k^{-1}(z+rd_{A}){\bmod {n}}}image hesaplanır. Eğer s=0{\displaystyle s=0}image ise 3.adıma geri dönülür.
  7. İmza çifte (r,s){\displaystyle (r,s)}image olur. Ayrıca (r,−smodn){\displaystyle (r,-s{\bmod {n}})}image de uygun bir imza çiftidir.

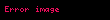
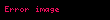
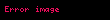
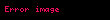
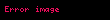
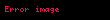
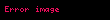
Standartların belirttiği gibi, k{\displaystyle k}image' nın sadece gizli olması yeterli değildir, aynı zamanda farklı imzalar için farklı k{\displaystyle k}image seçilmesi de önemlidir, aksi takdirde 6. adımdaki denklemde dA{\displaystyle d_{A}}image özel anahtarını çözülebilir: Bilinmeyen aynı k{\displaystyle k}image değeri ve bilinen iki farklı m{\displaystyle m}image ve m′{\displaystyle m'}image kullanılarak üretilen farklı iki imza olan (r,s){\displaystyle (r,s)}image ve (r,s′){\displaystyle (r,s')}image için saldırgan z{\displaystyle z}image ve z′{\displaystyle z'}image hesaplayabilir ve saldırgan s−s′=k−1(z−z′){\displaystyle s-s'=k^{-1}(z-z')}image formülünden k=z−z′s−s′{\displaystyle k={\frac {z-z'}{s-s'}}}image hesaplayabilir. Şimdi ise saldırgan s=k−1(z+rdA){\displaystyle s=k^{-1}(z+rd_{A})}image formülü üzerinde düzenleme yaparak özel anahtar olan dA=sk−zr{\displaystyle d_{A}={\frac {sk-z}{r}}}image' yı elde edebilir. Bu uygulama hatası, örneğin PlayStation 3 oyun konsolu için kullanılan imzalama anahtarını çıkarmak için kullanıldı. ECDSA imzasının özel anahtarları sızdırabilmesinin bir başka yolu, k{\displaystyle k}image hatalı bir rastgele sayı üreteci tarafından üretilir. Rastgele sayı üretmedeki bu tür bir başarısızlık, Android Bitcoin Cüzdan kullanıcılarının Ağustos 2013' te fonlarını kaybetmelerine neden oldu.k{\displaystyle k}image 'nın her mesaj için benzersiz olmasını sağlamak için, bir kişi rastgele sayı üretimini tamamen atlayabilir ve k{\displaystyle k}image 'yı hem mesajdan hem de özel anahtardan türeterek deterministik imzalar oluşturabilir.

İmza doğrulama algoritması

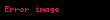
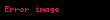
Bob'un Alice'in imzasını doğrulaması için açık anahtar eğri noktası olan QA{\displaystyle Q_{A}}image bir kopyasına sahip olması gerekir. Bob, QA{\displaystyle Q_{A}}image 'nun geçerli bir eğri noktası olduğunu şu şekilde doğrulayabilir:

  1. QA{\displaystyle Q_{A}}image nın O{\displaystyle O}image kimlik elemanına eşit olmadığını kontrol eder.
  2. QA{\displaystyle Q_{A}}image nın eğri üzerinde olduğunu kontrol eder.
  3. n×QA=O{\displaystyle n\times Q_{A}=O}image olduğunu kontrol eder.

Ardından Bob şu adımları izler:

  1. r{\displaystyle r}image ve s{\displaystyle s}image 'nin [1,n−1]{\displaystyle [1,n-1]}image aralığında tam sayılar olduğunu doğrular. Değilse, imza geçersizdir.
  2. e=HASH(m){\displaystyle e=HASH(m)}image 'yi hesaplar. Burada HASH imza üretirken kullanılan ile aynı kriptografik özet fonksiyonu temsil eder.
  3. z{\displaystyle z}image, e{\displaystyle e}image'in en solundaki bitleri olan Ln{\displaystyle L_{n}}image olsun
  4. w=s−1modn{\displaystyle w=s^{-1}{\bmod {n}}}image hesaplar.
  5. u1=zwmodn{\displaystyle u_{1}=zw{\bmod {n}}}image ve u2=rwmodn{\displaystyle u_{2}=rw{\bmod {n}}}image' yi hesaplar.
  6. (x1,y1)=u1×G+u2×QA{\displaystyle {\displaystyle (x_{1},y_{1})=u_{1}\times G+u_{2}\times Q_{A}}}imageeğri noktalarını hesaplar. Eğer (x1,y1)=O{\displaystyle {\displaystyle (x_{1},y_{1})=O}}image ise imza geçersizdir.
  7. Eğer r≡x1(modn){\displaystyle r\equiv x_{1}{\pmod {n}}}image ise imza geçerli, değilse geçersizdir.

Shamir' in numarasını kullanarak, iki skaler çarpımın toplamını yani 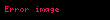u1×G+u2×QA{\displaystyle u_{1}\times G+u_{2}\times Q_{A}}image, bağımsız olarak yapılan iki skaler çarpımından daha hızlı hesaplanabileceğini unutmayın.

Algoritmanın doğruluğu

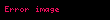
Doğrulamanın neden doğru şekilde çalıştığı çok belli değildir. Nedenini görmek için, doğrulamanın 6. adımında hesaplanan eğri noktasını C{\displaystyle C}image olarak belirtelim:

C=u1×G+u2×QA{\displaystyle C=u_{1}\times G+u_{2}\times Q_{A}}image

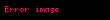
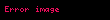
Açık anahtarın QA=dA×G{\displaystyle Q_{A}=d_{A}\times G}image tanımından,

C=u1×G+u2dA×G{\displaystyle C=u_{1}\times G+u_{2}d_{A}\times G}image

elde edilir. Eliptik eğride skaler çarpımın toplama üzerine dağılma özelliğinden,

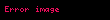
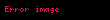
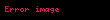
C=(u1+u2dA)×G{\displaystyle C=(u_{1}+u_{2}d_{A})\times G}image

u1{\displaystyle u_{1}}imageve u2{\displaystyle u_{2}}image' nin doğrulamanın 5.adımındaki tanımını açarsak,

C=(zs−1+rdAs−1)×G{\displaystyle C=(zs^{-1}+rd_{A}s^{-1})\times G}image

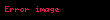
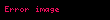
buradan s−1{\displaystyle s^{-1}}image parantezine alındığında,

C=(z+rdA)s−1×G{\displaystyle C=(z+rd_{A})s^{-1}\times G}image

s' nin imzanın 6. adımdaki tanımını açarsak,

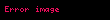
C=(z+rdA)(z+rdA)−1(k−1)−1×G{\displaystyle C=(z+rd_{A})(z+rd_{A})^{-1}(k^{-1})^{-1}\times G}image

Bir elemanın tersinin tersi kendisini verir ve bir elemanın tersi ile kendisinin çarpımı birim elemanı vereceğinden,

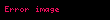
C=k×G{\displaystyle C=k\times G}image

r{\displaystyle r}image' nin tanımından bu, doğrulama adımı 7'dir.

Güvenlik

Aralık 2010'da, kendini "fail0verflow" diye adlandıran bir grup, Sony tarafından üretilen PlayStation 3 oyun konsolunun yazılımını imzalamak için kullanılan ECDSA özel anahtarının kırıldığını duyurdu ancak bu saldırı yalnızca Sony algoritmayı düzgün şekilde uygulamadığı için gerçekleşti çünkü k{\displaystyle k}image rastgele değil sabit seçilmişti. Yukarıdaki İmza oluşturma algoritması bölümünde belirtildiği gibi, bu, dA{\displaystyle d_{A}}image 'yı çözülebilir hale ve tüm algoritmayı işe yaramaz hale getirir.

29 Mart 2011 tarihinde, iki araştırmacı, bir zamanlama saldırısı yaparak binary alan üzerinden ECDSA ile kimlik doğrulaması yapan OpenSSL kullanarak sunucunun TLS özel anahtarını almanın mümkün olduğunu gösteren bir IACR makalesi yayınladı. Güvenlik açığı, OpenSSL 1.0.0e' de düzeltildi.

Ağustos 2013’te, Java sınıfının bazı uygulamalarındaki hataların bazen k{\displaystyle k}image değerinde ürettiği ortaya çıktı. Bu, bilgisayar korsanlarının, kendilerine ait anahtarların sahiplerinin sahip olduğu bitcoin işlemleri üzerinde aynı kontrolü sağlayan özel anahtarı kırma izin verdi; aynı şekilde, Java kullanan ve ECDSA' nın kimliğini doğrulamak için kullanan ve bazı Android uygulama uygulamalarında PS3 imzalama anahtarını ortaya çıkarmak için kullanıldı.

Bu sorun, RFC 6979 tarafından tanımlandığı gibi deterministik k{\displaystyle k}image üretimi ile önlenebilir.

Endişeler

ECDSA ile ilgili iki tür endişe vardır:

  1. Politik kaygılar: NIST'in ürettiği eğrilerin güvenilirliği, NSA' nın yazılımlarına, donanım bileşenlerine ve yayınlanmış standartlarına bilinçli bir şekilde arka kapı koymasının ardından, tanınmış kriptograflar, NIST eğrilerinin nasıl tasarlandığına dair şüphelerini dile getirdiler.
  2. Teknik kaygılar: Standartın doğru uygulama zorluğu, yavaşlığı ve Dual EC DRBG rastgele sayı üretecinin yetersiz savunma uygulamalarında güvenliği azaltan kusurların tasarlanması.

Bu sorunların her ikisi de libssh curved25519 giriş bölümünde özetlenmiştir.

Uygulamalar

Aşağıda, ECDSA'ya destek sağlayan şifreleme kütüphanelerinin bir listesi bulunmaktadır:

  • OpenSSL

Kaynakça

  1. ^ (PDF). 29 Ekim 2019 tarihinde kaynağından (PDF) arşivlendi. Erişim tarihi: 7 Nisan 2019. 
  2. ^ . 7 Nisan 2019 tarihinde kaynağından arşivlendi. Erişim tarihi: 7 Nisan 2019. 
  3. ^ rfc:6979
  4. ^ "Arşivlenmiş kopya". 7 Nisan 2019 tarihinde kaynağından . Erişim tarihi: 7 Nisan 2019. 
  5. ^ . 7 Nisan 2019 tarihinde kaynağından arşivlendi. Erişim tarihi: 7 Nisan 2019. 
  6. ^ "Arşivlenmiş kopya". 8 Aralık 2018 tarihinde kaynağından . Erişim tarihi: 7 Nisan 2019. 
  7. ^ "Arşivlenmiş kopya". 26 Şubat 2013 tarihinde kaynağından arşivlendi. Erişim tarihi: 7 Nisan 2019. 
  8. ^ . 15 Aralık 2017 tarihinde kaynağından arşivlendi. Erişim tarihi: 7 Nisan 2019. 
  9. ^ (PDF). 28 Mayıs 2019 tarihinde kaynağından (PDF) arşivlendi. Erişim tarihi: 7 Nisan 2019. 
  10. ^ . 7 Nisan 2019 tarihinde kaynağından arşivlendi. Erişim tarihi: 7 Nisan 2019. 
  11. ^ "Arşivlenmiş kopya". 7 Nisan 2019 tarihinde kaynağından . Erişim tarihi: 7 Nisan 2019. 
  12. ^ "Arşivlenmiş kopya". 23 Nisan 2019 tarihinde kaynağından . Erişim tarihi: 7 Nisan 2019. 
  13. ^ "Arşivlenmiş kopya". 23 Mart 2014 tarihinde kaynağından . Erişim tarihi: 7 Nisan 2019. 
  14. ^ . 19 Ağustos 2016 tarihinde kaynağından arşivlendi. Erişim tarihi: 7 Nisan 2019. 
  15. ^ . 23 Mart 2019 tarihinde kaynağından arşivlendi. Erişim tarihi: 7 Nisan 2019. 

wikipedia, wiki, viki, vikipedia, oku, kitap, kütüphane, kütübhane, ara, ara bul, bul, herşey, ne arasanız burada,hikayeler, makale, kitaplar, öğren, wiki, bilgi, tarih, yukle, izle, telefon için, turk, türk, türkçe, turkce, nasıl yapılır, ne demek, nasıl, yapmak, yapılır, indir, ücretsiz, ücretsiz indir, bedava, bedava indir, mp3, video, mp4, 3gp, jpg, jpeg, gif, png, resim, müzik, şarkı, film, film, oyun, oyunlar, mobil, cep telefonu, telefon, android, ios, apple, samsung, iphone, xiomi, xiaomi, redmi, honor, oppo, nokia, sonya, mi, pc, web, computer, bilgisayar

Kriptografide Eliptik Egri Dijital Imza Algoritmasi ECDSA eliptik egri sifrelemesi kullanan bircok cesit Dijital Imza Algoritmasi DSA sunar DSA ile anahtar ve imza boyut karsilastirmasiGenel olarak eliptik egri kriptografisinde oldugu gibi acik anahtarin bit boyutu ECDSA icin yeterli oldugu dusunulen guvenlik seviyesinin bitlerin yaklasik iki kati kadardir Ornegin 80 bitlik bir guvenlik duzeyinde bir ECDSA nin yani saldirganin gizli anahtari bulmak icin maksimum 280 displaystyle 2 80 operasyon deneme yapmasi gerektigi anlamina gelir genel anahtarinin boyutu 160 bit olurken bir DSA genel anahtarinin boyutu en az 1024 bit tir Ote yandan guvenlik seviyesinin t displaystyle t uzunlugunda oldugu hem DSA hem de ECDSA icin imza boyutu yaklasik 4t displaystyle 4t olur baska bir deyisle 80 bit guvenlik duzeyi icin yaklasik 320 bitlik imza gerekir Imza olusturma algoritmasiDiyelim ki imzali bir mesaj gondermek istiyor Ilk olarak egri parametreleri olan CURVE G n displaystyle displaystyle textrm CURVE G n uzerinde anlasmalidirlar Cisme ve egri esitligine ek olarak egri uzerinde asal mertebenin temel noktasi olan G ve G nin carpimsal mertebesi olan n ye ihtiyac vardir ParametreEGRI eliptik egri alani ve kullanilan denklemG eliptik egri taban noktasi or y2 x3 7 displaystyle y 2 x 3 7 n mertebeden cok buyuk bir asal ile eliptik egri ureticisi n G nin tam sayi mertebesi yani nxG O displaystyle nxG O burada O displaystyle O tanimlayici elemandir dA Rastgele secilmis gizli anahtarQa Eliptik egriden hesaplanmis acik anahtarm mesaj n displaystyle n asal bir sayi olmak zorundadir Aslinda Z nZ displaystyle mathbb Z n mathbb Z halkasinin sifirdan farkli her elemaninin tersine oldugunu varsayariz yani Z nZ displaystyle mathbb Z n mathbb Z cisim olmak zorundadir Buda bize n displaystyle n nin asal olmasi gerektigini gosterir bkn Bezout Teoremi Alice 1 n 1 displaystyle 1 n 1 araligindan rastgele secilmis ozel anahtar olan dA displaystyle d A yi ve egrinin public keyi olan QA dA G displaystyle Q A d A times G iceren bir anahtar cifti olusturur displaystyle times eliptik egri skaler nokta carpimini temsil eder Alice m displaystyle m mesajini imzalayabilmesi icin asagidaki adimlari takip etmelidir e HASH m displaystyle e HASH m yi hesaplar Burada HASH Kriptografik ozet fonksiyonu temsil eder z displaystyle z e displaystyle e in en solundaki bitleri olan Ln displaystyle L n olsun burada Ln displaystyle L n n mertebeden bir grubun mertebesi olsun 1 n 1 displaystyle 1 n 1 arasindan kriptografik olarak guvenli rastgele bir tam sayi k displaystyle k secer Egri noktalari olan x1 y1 k G displaystyle x 1 y 1 k times G hesaplar r x1modn displaystyle r x 1 bmod n hesaplanir Eger r 0 displaystyle r 0 ise 3 adima geri donulur s k 1 z rdA modn displaystyle s k 1 z rd A bmod n hesaplanir Eger s 0 displaystyle s 0 ise 3 adima geri donulur Imza cifte r s displaystyle r s olur Ayrica r smodn displaystyle r s bmod n de uygun bir imza ciftidir Standartlarin belirttigi gibi k displaystyle k nin sadece gizli olmasi yeterli degildir ayni zamanda farkli imzalar icin farkli k displaystyle k secilmesi de onemlidir aksi takdirde 6 adimdaki denklemde dA displaystyle d A ozel anahtarini cozulebilir Bilinmeyen ayni k displaystyle k degeri ve bilinen iki farkli m displaystyle m ve m displaystyle m kullanilarak uretilen farkli iki imza olan r s displaystyle r s ve r s displaystyle r s icin saldirgan z displaystyle z ve z displaystyle z hesaplayabilir ve saldirgan s s k 1 z z displaystyle s s k 1 z z formulunden k z z s s displaystyle k frac z z s s hesaplayabilir Simdi ise saldirgan s k 1 z rdA displaystyle s k 1 z rd A formulu uzerinde duzenleme yaparak ozel anahtar olan dA sk zr displaystyle d A frac sk z r yi elde edebilir Bu uygulama hatasi ornegin PlayStation 3 oyun konsolu icin kullanilan imzalama anahtarini cikarmak icin kullanildi ECDSA imzasinin ozel anahtarlari sizdirabilmesinin bir baska yolu k displaystyle k hatali bir rastgele sayi ureteci tarafindan uretilir Rastgele sayi uretmedeki bu tur bir basarisizlik Android Bitcoin Cuzdan kullanicilarinin Agustos 2013 te fonlarini kaybetmelerine neden oldu k displaystyle k nin her mesaj icin benzersiz olmasini saglamak icin bir kisi rastgele sayi uretimini tamamen atlayabilir ve k displaystyle k yi hem mesajdan hem de ozel anahtardan tureterek deterministik imzalar olusturabilir Imza dogrulama algoritmasiBob un Alice in imzasini dogrulamasi icin acik anahtar egri noktasi olan QA displaystyle Q A bir kopyasina sahip olmasi gerekir Bob QA displaystyle Q A nun gecerli bir egri noktasi oldugunu su sekilde dogrulayabilir QA displaystyle Q A nin O displaystyle O kimlik elemanina esit olmadigini kontrol eder QA displaystyle Q A nin egri uzerinde oldugunu kontrol eder n QA O displaystyle n times Q A O oldugunu kontrol eder Ardindan Bob su adimlari izler r displaystyle r ve s displaystyle s nin 1 n 1 displaystyle 1 n 1 araliginda tam sayilar oldugunu dogrular Degilse imza gecersizdir e HASH m displaystyle e HASH m yi hesaplar Burada HASH imza uretirken kullanilan ile ayni kriptografik ozet fonksiyonu temsil eder z displaystyle z e displaystyle e in en solundaki bitleri olan Ln displaystyle L n olsun w s 1modn displaystyle w s 1 bmod n hesaplar u1 zwmodn displaystyle u 1 zw bmod n ve u2 rwmodn displaystyle u 2 rw bmod n yi hesaplar x1 y1 u1 G u2 QA displaystyle displaystyle x 1 y 1 u 1 times G u 2 times Q A egri noktalarini hesaplar Eger x1 y1 O displaystyle displaystyle x 1 y 1 O ise imza gecersizdir Eger r x1 modn displaystyle r equiv x 1 pmod n ise imza gecerli degilse gecersizdir Shamir in numarasini kullanarak iki skaler carpimin toplamini yani u1 G u2 QA displaystyle u 1 times G u 2 times Q A bagimsiz olarak yapilan iki skaler carpimindan daha hizli hesaplanabilecegini unutmayin Algoritmanin dogruluguDogrulamanin neden dogru sekilde calistigi cok belli degildir Nedenini gormek icin dogrulamanin 6 adiminda hesaplanan egri noktasini C displaystyle C olarak belirtelim C u1 G u2 QA displaystyle C u 1 times G u 2 times Q A Acik anahtarin QA dA G displaystyle Q A d A times G tanimindan C u1 G u2dA G displaystyle C u 1 times G u 2 d A times G elde edilir Eliptik egride skaler carpimin toplama uzerine dagilma ozelliginden C u1 u2dA G displaystyle C u 1 u 2 d A times G u1 displaystyle u 1 ve u2 displaystyle u 2 nin dogrulamanin 5 adimindaki tanimini acarsak C zs 1 rdAs 1 G displaystyle C zs 1 rd A s 1 times G buradan s 1 displaystyle s 1 parantezine alindiginda C z rdA s 1 G displaystyle C z rd A s 1 times G s nin imzanin 6 adimdaki tanimini acarsak C z rdA z rdA 1 k 1 1 G displaystyle C z rd A z rd A 1 k 1 1 times G Bir elemanin tersinin tersi kendisini verir ve bir elemanin tersi ile kendisinin carpimi birim elemani vereceginden C k G displaystyle C k times G r displaystyle r nin tanimindan bu dogrulama adimi 7 dir GuvenlikAralik 2010 da kendini fail0verflow diye adlandiran bir grup Sony tarafindan uretilen PlayStation 3 oyun konsolunun yazilimini imzalamak icin kullanilan ECDSA ozel anahtarinin kirildigini duyurdu ancak bu saldiri yalnizca Sony algoritmayi duzgun sekilde uygulamadigi icin gerceklesti cunku k displaystyle k rastgele degil sabit secilmisti Yukaridaki Imza olusturma algoritmasi bolumunde belirtildigi gibi bu dA displaystyle d A yi cozulebilir hale ve tum algoritmayi ise yaramaz hale getirir 29 Mart 2011 tarihinde iki arastirmaci bir zamanlama saldirisi yaparak binary alan uzerinden ECDSA ile kimlik dogrulamasi yapan OpenSSL kullanarak sunucunun TLS ozel anahtarini almanin mumkun oldugunu gosteren bir IACR makalesi yayinladi Guvenlik acigi OpenSSL 1 0 0e de duzeltildi Agustos 2013 te Java sinifinin bazi uygulamalarindaki hatalarin bazen k displaystyle k degerinde urettigi ortaya cikti Bu bilgisayar korsanlarinin kendilerine ait anahtarlarin sahiplerinin sahip oldugu bitcoin islemleri uzerinde ayni kontrolu saglayan ozel anahtari kirma izin verdi ayni sekilde Java kullanan ve ECDSA nin kimligini dogrulamak icin kullanan ve bazi Android uygulama uygulamalarinda PS3 imzalama anahtarini ortaya cikarmak icin kullanildi Bu sorun RFC 6979 tarafindan tanimlandigi gibi deterministik k displaystyle k uretimi ile onlenebilir EndiselerECDSA ile ilgili iki tur endise vardir Politik kaygilar NIST in urettigi egrilerin guvenilirligi NSA nin yazilimlarina donanim bilesenlerine ve yayinlanmis standartlarina bilincli bir sekilde arka kapi koymasinin ardindan taninmis kriptograflar NIST egrilerinin nasil tasarlandigina dair suphelerini dile getirdiler Teknik kaygilar Standartin dogru uygulama zorlugu yavasligi ve Dual EC DRBG rastgele sayi uretecinin yetersiz savunma uygulamalarinda guvenligi azaltan kusurlarin tasarlanmasi Bu sorunlarin her ikisi de libssh curved25519 giris bolumunde ozetlenmistir UygulamalarAsagida ECDSA ya destek saglayan sifreleme kutuphanelerinin bir listesi bulunmaktadir OpenSSLKaynakca PDF 29 Ekim 2019 tarihinde kaynagindan PDF arsivlendi Erisim tarihi 7 Nisan 2019 7 Nisan 2019 tarihinde kaynagindan arsivlendi Erisim tarihi 7 Nisan 2019 rfc 6979 Arsivlenmis kopya 7 Nisan 2019 tarihinde kaynagindan Erisim tarihi 7 Nisan 2019 7 Nisan 2019 tarihinde kaynagindan arsivlendi Erisim tarihi 7 Nisan 2019 Arsivlenmis kopya 8 Aralik 2018 tarihinde kaynagindan Erisim tarihi 7 Nisan 2019 Arsivlenmis kopya 26 Subat 2013 tarihinde kaynagindan arsivlendi Erisim tarihi 7 Nisan 2019 15 Aralik 2017 tarihinde kaynagindan arsivlendi Erisim tarihi 7 Nisan 2019 PDF 28 Mayis 2019 tarihinde kaynagindan PDF arsivlendi Erisim tarihi 7 Nisan 2019 7 Nisan 2019 tarihinde kaynagindan arsivlendi Erisim tarihi 7 Nisan 2019 Arsivlenmis kopya 7 Nisan 2019 tarihinde kaynagindan Erisim tarihi 7 Nisan 2019 Arsivlenmis kopya 23 Nisan 2019 tarihinde kaynagindan Erisim tarihi 7 Nisan 2019 Arsivlenmis kopya 23 Mart 2014 tarihinde kaynagindan Erisim tarihi 7 Nisan 2019 19 Agustos 2016 tarihinde kaynagindan arsivlendi Erisim tarihi 7 Nisan 2019 23 Mart 2019 tarihinde kaynagindan arsivlendi Erisim tarihi 7 Nisan 2019

Yayın tarihi: Temmuz 21, 2024, 18:42 pm
En çok okunan
  • Aralık 11, 2025

    TimedText:Loxodonta africana oral rumble visualized with acoustic camera (25fps) - pone.0048907.s003.ogv

  • Aralık 12, 2025

    TimedText:Great Blue Heron.ogg

  • Aralık 11, 2025

    TimedText:En-us-Saint Kitts and Nevis.ogg

  • Aralık 10, 2025

    TimedText:En-ca-Canada.ogg

  • Aralık 11, 2025

    TimedText:ElKanunfitTıb.ogg

Günlük

  • Vikipedi

  • Erdem Kınay

  • Avrupa

  • 1545

  • Trento Konsili

  • Ernst Werner von Siemens

  • Riccardo Ehrman

  • Günter Schabowski

  • Berlin Duvarı

  • Fransa'nın illeri

NiNa.Az - Stüdyo

  • Vikipedi

Bültene üye ol

Mail listemize abone olarak bizden her zaman en son haberleri alacaksınız.
Temasta ol
Bize Ulaşın
DMCA Sitemap Feeds
© 2019 nina.az - Her hakkı saklıdır.
Telif hakkı: Dadaş Mammedov
Üst