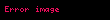Einstein-Hilbert etkisi (Hilbert etkisi olarak da adlandırılır) genel görelilikte en küçük eylem ilkesi boyunca Einstein alan denklemleri üretir. Hilbert etkisi genel görelilikte yerçekiminin dinamiğini tarifleyen fonksiyonel işlemdir., etkinin çekimsel kısmı,
burada metrik tensor determinantı, R Ricci sayılabilir büyüklüğü ve burada G Newton çekim sabiti ve c vakum içindeki ışık hızı şeklinde verilir. Eğer integral yakınsanıyorsa, tüm uzay zaman üzerinde alınır. Eğer yakınsamıyorsa S tanımlanamaz ama modife edilmiş tanımda bir integral isteğe bağlı şekilde büyük, bağıl tıkız tanım kümesinde yine Einstein denklemini Einstein Hilber ekisinin Euler- Lagrange denklemi olarak üretir.
Bu etki ilk kez David Hilbert tarafından 1915'te ileri sürülmüştür.
Tartışma
Etkiden ötürü denklemlerin türevi bazı avantajlara sahip. İlk olarak, Maxwell teorisi gibi etki olarak formüle edilmiş klasik alan teorileriyle genel göreliliğin kolayca birleşimine izin verir. Etkiden türevleme süreci madde alanlarına metrik bağlantı kaynağı tanımı için doğal adayı tanımlar. Ayrıca, bu etki kolay tanımlı korunan nicelikler için Noether'in teorisi boyunca etkinin simetrik çalışmasına izin verir.
Genel görelelikte, bu etki genellikle metrik ve maddesel alanların işlevseli olduğu varsayılır ve bağlantı Levi- Civita bağıntısı ile verilir. Genel göreliliğin Palatini formülasyonu metric ve bağlantının bağımsız olduğunu ve bağlı olmayan spinle fermionic madde alanlarını kapsamayı mümkün kılan ikisine göre bağımsız değişkenler varsayar.
Maddenin varlığındaki Einstein denklemleri madde etkisini Einstein- Hilbert etkisine eklenmesiyle verilir.
Einstein Denklemlerinin Türevi
Teorinin tüm etkisi Einstein- Hilbert terimi artı terim 
Etki prensibi bize bu etkinin ters metriğe göre değişkeni sıfır der,
Çünkü bu eşitlik her 
metric alan için hareket denklemi. Denklemin sağ tarafı tanımdan stres- enerji tensorüyle orantılı,
Denklemin sol tarafını hesaplamak için metric determinant ve Ricci sayılabilir büyüklüğünün değişkenlerine ihtiyacımız var. Bunlar standart ders kitabı hesaplamalarından elde edilebilir.
Riemann tensoru, Ricci tensoru ve Ricci sıkaler Değişkeni
hesaplamak için önce Riemann eğrilik tensor değişkenini hesaplarız ve sonra da Ricci tensor değişkenini. Böylece Riemann eğrilik tensoru;
olarak tanımlanır.
Riemann tensor değişkeni
olarak hesaplanabilir çünkü Riemann eğriliği sadece levi- Civita bağıntısına 
Şimdi, bu bir tensor ve biz bunun eşdeğişken türevini hesaplayabiliriz çünkü 
Biz şimdi yukardaki Riemann eğrilik tensoru değişkeni ifadesinin;
bu iki terimin farkına eşit olduğunu söyleyebiliriz.
Biz şimdi Ricci eğrilik tensorunun değişkenini basitce Riemann tensor değişkenini ik indeksinin daralması vasıtasıyla elde edebilir ve Palatini özdeşliğini bulabiliriz.
Ricci sıkaler;
olarak tanımlanır.
Sonuç olarak, ters metric 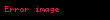
vasıtasıyla verilir.
İkinci satırda Ricci eğrilik değişkeni ve eşdeğişken türevin, 
Son terim, 

ve böylece sadece Stokes teoremi vasıtasıyla integral alındığında limit terim üretir. Bu yüzden sonsuzda metric değişken yok olduğu zaman, bu terim etki değişkenine katkıda bulunmaz. Ve böylece;
Determinant Değişimi
Jacobi formülü, determinant türev kuralı,
verir ya da koordinat sistemi 
Bunu kullanarak,
buluruz.
Son eşitlikte,
ters matrix türevi kuralından gelen
olgusunu kullandık.
Böylece
Hareket Denklemi
Şimdi emrimizdeki tüm önemli değişkenlere sahibiz, onları hareket denklemi içine metrik alan elde etmek için ekleyebiliriz.
Einstein alan denklemi ve
seçilen relativistik olmayan limite kadar Newton'un her zamanki çekim yasasını üretir, G çekimsel sabit.
Kozmolojik Sabit
Bazen yeni etki için kozmolojik sabit /\ ' e Lagrangian dahil edilebilir,
alan denklemleri üretir.
Kaynakça
- ^ Schreiber, Urs (20 Ocak 2015). . nLab. 11 Haziran 2015 tarihinde kaynağından arşivlendi. Erişim tarihi: 20 Haziran 2015.
İngilizce vikipedi.
wikipedia, wiki, viki, vikipedia, oku, kitap, kütüphane, kütübhane, ara, ara bul, bul, herşey, ne arasanız burada,hikayeler, makale, kitaplar, öğren, wiki, bilgi, tarih, yukle, izle, telefon için, turk, türk, türkçe, turkce, nasıl yapılır, ne demek, nasıl, yapmak, yapılır, indir, ücretsiz, ücretsiz indir, bedava, bedava indir, mp3, video, mp4, 3gp, jpg, jpeg, gif, png, resim, müzik, şarkı, film, film, oyun, oyunlar, mobil, cep telefonu, telefon, android, ios, apple, samsung, iphone, xiomi, xiaomi, redmi, honor, oppo, nokia, sonya, mi, pc, web, computer, bilgisayar
Einstein Hilbert etkisi Hilbert etkisi olarak da adlandirilir genel gorelilikte en kucuk eylem ilkesi boyunca Einstein alan denklemleri uretir Hilbert etkisi genel gorelilikte yercekiminin dinamigini tarifleyen fonksiyonel islemdir etkinin cekimsel kismi S 12k R gd4x displaystyle S 1 over 2 kappa int R sqrt g mathrm d 4 x burada g det gmn displaystyle g det g mu nu metrik tensor determinanti R Ricci sayilabilir buyuklugu ve k 8pGc 4 displaystyle kappa 8 pi Gc 4 burada G Newton cekim sabiti ve c vakum icindeki isik hizi seklinde verilir Eger integral yakinsaniyorsa tum uzay zaman uzerinde alinir Eger yakinsamiyorsa S tanimlanamaz ama modife edilmis tanimda bir integral istege bagli sekilde buyuk bagil tikiz tanim kumesinde yine Einstein denklemini Einstein Hilber ekisinin Euler Lagrange denklemi olarak uretir Bu etki ilk kez David Hilbert tarafindan 1915 te ileri surulmustur TartismaEtkiden oturu denklemlerin turevi bazi avantajlara sahip Ilk olarak Maxwell teorisi gibi etki olarak formule edilmis klasik alan teorileriyle genel goreliligin kolayca birlesimine izin verir Etkiden turevleme sureci madde alanlarina metrik baglanti kaynagi tanimi icin dogal adayi tanimlar Ayrica bu etki kolay tanimli korunan nicelikler icin Noether in teorisi boyunca etkinin simetrik calismasina izin verir Genel gorelelikte bu etki genellikle metrik ve maddesel alanlarin islevseli oldugu varsayilir ve baglanti Levi Civita bagintisi ile verilir Genel goreliligin Palatini formulasyonu metric ve baglantinin bagimsiz oldugunu ve bagli olmayan spinle fermionic madde alanlarini kapsamayi mumkun kilan ikisine gore bagimsiz degiskenler varsayar Maddenin varligindaki Einstein denklemleri madde etkisini Einstein Hilbert etkisine eklenmesiyle verilir Einstein Denklemlerinin TureviTeorinin tum etkisi Einstein Hilbert terimi arti terim LM displaystyle mathcal L mathrm M teoride gorulen herhangi madde alanlari tanimiyla verilsin S 12kR LM gd4x displaystyle S int left 1 over 2 kappa R mathcal L mathrm M right sqrt g mathrm d 4 x Etki prensibi bize bu etkinin ters metrige gore degiskeni sifir der 0 dS 12kd gR dgmn d gLM dgmn dgmnd4x 12k dRdgmn R gd gdgmn 1 gd gLM dgmn dgmn gd4x displaystyle begin aligned 0 amp delta S amp int left 1 over 2 kappa frac delta sqrt g R delta g mu nu frac delta sqrt g mathcal L mathrm M delta g mu nu right delta g mu nu mathrm d 4 x amp int left 1 over 2 kappa left frac delta R delta g mu nu frac R sqrt g frac delta sqrt g delta g mu nu right frac 1 sqrt g frac delta sqrt g mathcal L mathrm M delta g mu nu right delta g mu nu sqrt g mathrm d 4 x end aligned Cunku bu esitlik her dgmn displaystyle delta g mu nu icin gecerli olmali sunu der dRdgmn R gd gdgmn 2k1 gd gLM dgmn displaystyle frac delta R delta g mu nu frac R sqrt g frac delta sqrt g delta g mu nu 2 kappa frac 1 sqrt g frac delta sqrt g mathcal L mathrm M delta g mu nu metric alan icin hareket denklemi Denklemin sag tarafi tanimdan stres enerji tensoruyle orantili Tmn 2 gd gLM dgmn 2dLMdgmn gmnLM displaystyle T mu nu frac 2 sqrt g frac delta sqrt g mathcal L mathrm M delta g mu nu 2 frac delta mathcal L mathrm M delta g mu nu g mu nu mathcal L mathrm M Denklemin sol tarafini hesaplamak icin metric determinant ve Ricci sayilabilir buyuklugunun degiskenlerine ihtiyacimiz var Bunlar standart ders kitabi hesaplamalarindan elde edilebilir Riemann tensoru Ricci tensoru ve Ricci sikaler Degiskeni hesaplamak icin once Riemann egrilik tensor degiskenini hesaplariz ve sonra da Ricci tensor degiskenini Boylece Riemann egrilik tensoru Rrsmn mGnsr nGmsr GmlrGnsl GnlrGmsl displaystyle R rho sigma mu nu partial mu Gamma nu sigma rho partial nu Gamma mu sigma rho Gamma mu lambda rho Gamma nu sigma lambda Gamma nu lambda rho Gamma mu sigma lambda olarak tanimlanir Riemann tensor degiskeni dRrsmn mdGnsr ndGmsr dGmlrGnsl GmlrdGnsl dGnlrGmsl GnlrdGmsl displaystyle delta R rho sigma mu nu partial mu delta Gamma nu sigma rho partial nu delta Gamma mu sigma rho delta Gamma mu lambda rho Gamma nu sigma lambda Gamma mu lambda rho delta Gamma nu sigma lambda delta Gamma nu lambda rho Gamma mu sigma lambda Gamma nu lambda rho delta Gamma mu sigma lambda olarak hesaplanabilir cunku Riemann egriligi sadece levi Civita bagintisina Gmnl displaystyle Gamma mu nu lambda bagli Simdi bu bir tensor ve biz bunun esdegisken turevini hesaplayabiliriz cunku dGnmr displaystyle delta Gamma nu mu rho iki bagintinin farki l dGnmr l dGnmr GslrdGnms GnlsdGsmr GmlsdGnsr displaystyle nabla lambda delta Gamma nu mu rho partial lambda delta Gamma nu mu rho Gamma sigma lambda rho delta Gamma nu mu sigma Gamma nu lambda sigma delta Gamma sigma mu rho Gamma mu lambda sigma delta Gamma nu sigma rho Biz simdi yukardaki Riemann egrilik tensoru degiskeni ifadesinin dRrsmn m dGnsr n dGmsr displaystyle delta R rho sigma mu nu nabla mu delta Gamma nu sigma rho nabla nu delta Gamma mu sigma rho bu iki terimin farkina esit oldugunu soyleyebiliriz Biz simdi Ricci egrilik tensorunun degiskenini basitce Riemann tensor degiskenini ik indeksinin daralmasi vasitasiyla elde edebilir ve Palatini ozdesligini bulabiliriz dRmn dRrmrn r dGnmr n dGrmr displaystyle delta R mu nu equiv delta R rho mu rho nu nabla rho delta Gamma nu mu rho nabla nu delta Gamma rho mu rho Ricci sikaler R gmnRmn displaystyle R g mu nu R mu nu olarak tanimlanir Sonuc olarak ters metric gmn displaystyle g mu nu e gore degisken dR Rmndgmn gmndRmn Rmndgmn s gmndGnms gmsdGrmr displaystyle begin aligned delta R amp R mu nu delta g mu nu g mu nu delta R mu nu amp R mu nu delta g mu nu nabla sigma left g mu nu delta Gamma nu mu sigma g mu sigma delta Gamma rho mu rho right end aligned vasitasiyla verilir Ikinci satirda Ricci egrilik degiskeni ve esdegisken turevin sgmn 0 displaystyle nabla sigma g mu nu 0 metric uygunlugu icin onceden elde edilmis sonucu kullandik Son terim s gmndGnms gmsdGrmr displaystyle nabla sigma g mu nu delta Gamma nu mu sigma g mu sigma delta Gamma rho mu rho g displaystyle sqrt g le carpilan total tureve donustu gA aa gAa aor g mAm m gAm displaystyle sqrt g A a a sqrt g A a a mathrm or sqrt g nabla mu A mu partial mu left sqrt g A mu right ve boylece sadece Stokes teoremi vasitasiyla integral alindiginda limit terim uretir Bu yuzden sonsuzda metric degisken yok oldugu zaman bu terim etki degiskenine katkida bulunmaz Ve boylece dRdgmn Rmn displaystyle frac delta R delta g mu nu R mu nu Determinant Degisimi Jacobi formulu determinant turev kurali dg ddet gmn ggmndgmn displaystyle delta g delta det g mu nu g g mu nu delta g mu nu verir ya da koordinat sistemi gmn displaystyle g mu nu kosegen oldugu yere donusebilir ve sonra ana kosegenin elemanlarinin carpimi turevine carpma kurali uygular Bunu kullanarak d g 12 gdg 12 g gmndgmn 12 g gmndgmn displaystyle begin aligned delta sqrt g amp frac 1 2 sqrt g delta g amp frac 1 2 sqrt g g mu nu delta g mu nu amp frac 1 2 sqrt g g mu nu delta g mu nu end aligned buluruz Son esitlikte gmndgmn gmndgmn displaystyle g mu nu delta g mu nu g mu nu delta g mu nu ters matrix turevi kuralindan gelen dgmn gma dgab gbn displaystyle delta g mu nu g mu alpha delta g alpha beta g beta nu olgusunu kullandik Boylece 1 gd gdgmn 12gmn displaystyle frac 1 sqrt g frac delta sqrt g delta g mu nu frac 1 2 g mu nu Hareket Denklemi Simdi emrimizdeki tum onemli degiskenlere sahibiz onlari hareket denklemi icine metrik alan elde etmek icin ekleyebiliriz Rmn 12gmnR 8pGc4Tmn displaystyle R mu nu frac 1 2 g mu nu R frac 8 pi G c 4 T mu nu Einstein alan denklemi ve k 8pGc4 displaystyle kappa frac 8 pi G c 4 secilen relativistik olmayan limite kadar Newton un her zamanki cekim yasasini uretir G cekimsel sabit Kozmolojik Sabit Bazen yeni etki icin kozmolojik sabit e Lagrangian dahil edilebilir S 12k R 2L LM gd4x displaystyle S int left 1 over 2 kappa left R 2 Lambda right mathcal L mathrm M right sqrt g mathrm d 4 x Rmn 12gmnR Lgmn 8pGc4Tmn displaystyle R mu nu frac 1 2 g mu nu R Lambda g mu nu frac 8 pi G c 4 T mu nu alan denklemleri uretir Kaynakca Schreiber Urs 20 Ocak 2015 nLab 11 Haziran 2015 tarihinde kaynagindan arsivlendi Erisim tarihi 20 Haziran 2015 Ingilizce vikipedi
 Azərbaycanca
Azərbaycanca Deutsch
Deutsch 日本語
日本語 Lietuvos
Lietuvos සිංහල
සිංහල Türkçe
Türkçe Українська
Українська United State
United State