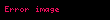Adını İngiliz fizikçi Paul Dirac'tan alan spinli ve göreli kuantum mekaniği denklemi,
şeklinde ifade edilebilir. Burada;
- m_0 : parçacığın durağan kütlesini,
- c : ışık hızını,
- : ,
- :
göstermektedir. Ayrıca , dört tane karmaşık sayıdan oluşan bir kolon matristir ve olasılığın dalga fonksiyonudur. Bu dört sayı da iki gruba ayrılır:
Buradaki ve , olarak adlandırılır ve her birinin farklı bir fiziksel anlamı vardır. , pozitif enerjileri, negatif enerjileri ifāde eder. Bunlar da
ve
olarak tanımlanır. ve olarak anlam kazanır. Yani, dalga fonksiyonu;
şeklindedir.
Serbest parçacık için Dirac denklemi
Dırac denklemlerinde 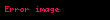
biçiminde yazılabilir. ; I, birim matris olmak üzere
ve
olarak Pauli matrisleri cinsinden yazılabilir. Bunlar yerine konunca Dirac denklemi,
biçimini alır. Matris çarpımı yapılırsa, denklemler elde edilir:
Bu özdeğer denklemlerini çözmek için, dönücülerden biri çekilip diğer denklemde yerine yazılabilir. Buradan, göreliliğin en önemli denklemlerinden biri elde edilir:
Burada 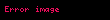

şeklindedir. Buradan E için pozitif ve negatif değerler gelir.
Elektromanyetik alanda Dirac denklemi
Denklemdeki dörtmomentum işlemcisine elektromanyetik potansiyeli dahil edersek:
denklem,
biçimine gelir. Buradaki 
 | Fizik ile ilgili bu madde seviyesindedir. Madde içeriğini genişleterek Vikipedi'ye katkı sağlayabilirsiniz. |
wikipedia, wiki, viki, vikipedia, oku, kitap, kütüphane, kütübhane, ara, ara bul, bul, herşey, ne arasanız burada,hikayeler, makale, kitaplar, öğren, wiki, bilgi, tarih, yukle, izle, telefon için, turk, türk, türkçe, turkce, nasıl yapılır, ne demek, nasıl, yapmak, yapılır, indir, ücretsiz, ücretsiz indir, bedava, bedava indir, mp3, video, mp4, 3gp, jpg, jpeg, gif, png, resim, müzik, şarkı, film, film, oyun, oyunlar, mobil, cep telefonu, telefon, android, ios, apple, samsung, iphone, xiomi, xiaomi, redmi, honor, oppo, nokia, sonya, mi, pc, web, computer, bilgisayar
Adini Ingiliz fizikci Paul Dirac tan alan spinli ve goreli kuantum mekanigi denklemi gmpmcPS m0c2PS displaystyle gamma mu p mu c mathbf Psi m 0 c 2 mathbf Psi seklinde ifade edilebilir Burada m 0 parcacigin duragan kutlesini c isik hizini pm displaystyle p mu gm displaystyle gamma mu dd gostermektedir Ayrica PS displaystyle Psi dort tane karmasik sayidan olusan bir kolon matristir ve olasiligin dalga fonksiyonudur Bu dort sayi da iki gruba ayrilir PS PS PS displaystyle Psi begin bmatrix Psi Psi end bmatrix dd Buradaki PS displaystyle Psi ve PS displaystyle Psi olarak adlandirilir ve her birinin farkli bir fiziksel anlami vardir PS displaystyle Psi pozitif enerjileri PS displaystyle Psi negatif enerjileri ifade eder Bunlar da PS ps ϕ displaystyle Psi begin bmatrix psi phi end bmatrix ve PS ps ϕ displaystyle Psi begin bmatrix psi phi end bmatrix dd olarak tanimlanir ps displaystyle psi ve ϕ displaystyle phi olarak anlam kazanir Yani dalga fonksiyonu PS ps ϕ ps ϕ displaystyle Psi begin bmatrix psi phi psi phi end bmatrix dd seklindedir Serbest parcacik icin Dirac denklemiDirac denklemlerinde m 0 displaystyle mu 0 bilesenini ayirip gerisi icin i 1 2 3 indisini birakirsak bknz Minkowski uzayzamani Dirac denklemi g0p0cPS gipicPS m0c2PS displaystyle gamma 0 p 0 c mathbf Psi gamma i p i c mathbf Psi m 0 c 2 mathbf Psi biciminde yazilabilir I birim matris olmak uzere g0 0II0 displaystyle gamma 0 begin bmatrix 0 amp amp I I amp amp 0 end bmatrix ve gi 0si si0 displaystyle gamma i begin bmatrix 0 amp amp sigma i sigma i amp amp 0 end bmatrix olarak Pauli matrisleri cinsinden yazilabilir Bunlar yerine konunca Dirac denklemi 0p0c sipicp0c sipic0 PS PS m0c2 PS PS displaystyle begin bmatrix 0 amp amp p 0 c sigma i p i c p 0 c sigma i p i c amp amp 0 end bmatrix begin bmatrix Psi Psi end bmatrix m 0 c 2 begin bmatrix Psi Psi end bmatrix bicimini alir Matris carpimi yapilirsa denklemler elde edilir p0c sipic PS m0c2PS displaystyle left p 0 c sigma i p i c right Psi m 0 c 2 Psi p0c sipic PS m0c2PS displaystyle left p 0 c sigma i p i c right Psi m 0 c 2 Psi Bu ozdeger denklemlerini cozmek icin donuculerden biri cekilip diger denklemde yerine yazilabilir Buradan goreliligin en onemli denklemlerinden biri elde edilir p02c2 pi2c2 m02c4 displaystyle p 0 2 c 2 p i 2 c 2 m 0 2 c 4 Burada p0c E mc2 displaystyle p 0 c E mc 2 ve pi2 p12 p22 p32 p 2 displaystyle p i 2 p 1 2 p 2 2 p 3 2 mathbf p 2 oldugundan ifade E2 p 2c2 m02c4 displaystyle E 2 mathbf p 2 c 2 m 0 2 c 4 seklindedir Buradan E icin pozitif ve negatif degerler gelir Elektromanyetik alanda Dirac denklemiDenklemdeki dortmomentum islemcisine elektromanyetik potansiyeli dahil edersek pm pm ecAm displaystyle p mu rightarrow p mu frac e c A mu denklem gm pmc eAm PS m0c2PS displaystyle gamma mu left p mu c eA mu right mathbf Psi m 0 c 2 mathbf Psi bicimine gelir Buradaki Am displaystyle A mu ve e elektriksel yuktur Fizik ile ilgili bu madde taslak seviyesindedir Madde icerigini genisleterek Vikipedi ye katki saglayabilirsiniz
 Azərbaycanca
Azərbaycanca Deutsch
Deutsch 日本語
日本語 Lietuvos
Lietuvos සිංහල
සිංහල Türkçe
Türkçe Українська
Українська United State
United State