Matematiğin bir alt dalı olan doğrusal cebirde, bir matrisinin devriği ya da transpozu bu matrisin satırları ile sütunları karşılıklı yer değiştirilmesiyle elde edilen matrise denilir. Devriği alınmış bir matrise devrik matris denilir. Bir matrisinin devriği genellikle transpoz karşılığından hareketle şeklinde ifade edilir; ancak, kullanılan diğer gösterimler arasında , ve de vardır. Bir matrisin devriği aşağıdaki biçimlerde elde edilebilir:
- matrisinin göre yansıması alınarak elde edilir,
- matrisinin satırları matrisinin sütünları olarak yazılarak elde edilir,
- matrisinin sütünları matrisinin satırları olarak yazılarak elde edilir.
matrisinin ögesi matrisinin ile gösterilen ögesine eşittir:
Eğer matrisi bir matris ise matrisi bir matristir. Bir sayılın (skaler) devriği yine o sayıldır.
Örnekler
Özellikler



- Bir matrisin devriğinin devriği kendisidir.
- Toplama işlemine göre yukardaki gibi dağıtılabilir.
- Matris çarpımının devriği yukardaki gibidir; matrislerin çarpımının sırası değişir ve iki matrisin de devriği alınır. Matris çarpımında sıra değişikliğine dikkat edilmesi gereklidir.
- Sayıl ile matris çarpımının devriği alınırken sayıl olduğu gibi bırakılır ve matrisin devriği alınır. Sayılın devriği kendisine eşittir ve matris ile sayıl çarpılırken çarpımın sırası önemli değildir.
- Kare bir matris için matrisin ile o matrisin devriğinin determinantı aynıdır.
- İki
ve
vektörünün, nokta çarpımı aşağıdaki gibi hesaplanabilir:
şeklinde Einstein gösterimi kullanılarak yazılabilir. Burada
alt imi ve
üst iminin aynı olması
üzerinden toplama yapılacağı manasına gelmektedir.
- Tersi alınabilir bir matrisin devriğinin de tersi alınabilir. Yukarıdaki
matrisinin devriğinin tersi ile tersinin devriği birbirine eşittir. Herhangi bir matrisin tersinin devriğinin tersi kendisine eşittir.
şeklinde yazım yukardaki eşitlikteki sağ veya sol taraftaki terimlerden herhangi birini ifade etmek için kullanılır.
- Tersi alınabilir bir matrisin devriğinin de tersi alınabilir. Yukarıdaki
- Eğer
kare bir matris ise bu matrisin özdeğerleri ile devriklerinin özdeğerleri birbirine eşittir.
Kaynakça
wikipedia, wiki, viki, vikipedia, oku, kitap, kütüphane, kütübhane, ara, ara bul, bul, herşey, ne arasanız burada,hikayeler, makale, kitaplar, öğren, wiki, bilgi, tarih, yukle, izle, telefon için, turk, türk, türkçe, turkce, nasıl yapılır, ne demek, nasıl, yapmak, yapılır, indir, ücretsiz, ücretsiz indir, bedava, bedava indir, mp3, video, mp4, 3gp, jpg, jpeg, gif, png, resim, müzik, şarkı, film, film, oyun, oyunlar, mobil, cep telefonu, telefon, android, ios, apple, samsung, iphone, xiomi, xiaomi, redmi, honor, oppo, nokia, sonya, mi, pc, web, computer, bilgisayar
Matematigin bir alt dali olan dogrusal cebirde bir A displaystyle A matrisinin devrigi ya da transpozu bu matrisin satirlari ile sutunlari karsilikli yer degistirilmesiyle elde edilen matrise denilir Devrigi alinmis bir matrise devrik matris denilir Bir A displaystyle A matrisinin devrigi genellikle transpoz karsiligindan hareketle At displaystyle A t seklinde ifade edilir ancak kullanilan diger gosterimler arasinda A displaystyle A Atr displaystyle A tr ve AT displaystyle A T de vardir Bir matrisin devrigi asagidaki bicimlerde elde edilebilir A displaystyle A matrisinin gore yansimasi alinarak At displaystyle A t elde edilir A displaystyle A matrisinin satirlari At displaystyle A t matrisinin sutunlari olarak yazilarak elde edilir A displaystyle A matrisinin sutunlari At displaystyle A t matrisinin satirlari olarak yazilarak elde edilir At displaystyle A t matrisinin i j displaystyle i j ogesi A displaystyle A matrisinin j i displaystyle j i ile gosterilen ogesine esittir AT ij A ji displaystyle A T ij A ji Eger A displaystyle A matrisi m n displaystyle m times n bir matris ise At displaystyle A t matrisi b m displaystyle b times m bir matristir Bir sayilin skaler devrigi yine o sayildir Ornekler 12 T 12 displaystyle begin bmatrix 1 amp 2 end bmatrix mathrm T begin bmatrix 1 2 end bmatrix 1234 T 1324 displaystyle begin bmatrix 1 amp 2 3 amp 4 end bmatrix mathrm T begin bmatrix 1 amp 3 2 amp 4 end bmatrix 123456 T 135246 displaystyle begin bmatrix 1 amp 2 3 amp 4 5 amp 6 end bmatrix mathrm T begin bmatrix 1 amp 3 amp 5 2 amp 4 amp 6 end bmatrix OzelliklerA displaystyle A B displaystyle B matrisleri ve c displaystyle c sayili icin asagidaki ozellikler gecerlidir AT T A displaystyle A T T A quad Bir matrisin devriginin devrigi kendisidir A B T AT BT displaystyle A B T A T B T Toplama islemine gore yukardaki gibi dagitilabilir AB T BTAT displaystyle left AB right T B T A T Matris carpiminin devrigi yukardaki gibidir matrislerin carpiminin sirasi degisir ve iki matrisin de devrigi alinir Matris carpiminda sira degisikligine dikkat edilmesi gereklidir cA T cAT displaystyle cA T cA T Sayil ile matris carpiminin devrigi alinirken sayil oldugu gibi birakilir ve matrisin devrigi alinir Sayilin devrigi kendisine esittir ve matris ile sayil carpilirken carpimin sirasi onemli degildir det AT det A displaystyle det A T det A Kare bir matris icin matrisin ile o matrisin devriginin determinanti aynidir Iki a displaystyle a ve b displaystyle b vektorunun nokta carpimi asagidaki gibi hesaplanabilir a b aTb displaystyle a cdot b a T b Bu carpimda aibi displaystyle a i b i seklinde Einstein gosterimi kullanilarak yazilabilir Burada i displaystyle i alt imi ve i displaystyle i ust iminin ayni olmasi i displaystyle i uzerinden toplama yapilacagi manasina gelmektedir AT 1 A 1 T displaystyle A T 1 A 1 T Tersi alinabilir bir matrisin devriginin de tersi alinabilir Yukaridaki A displaystyle A matrisinin devriginin tersi ile tersinin devrigi birbirine esittir Herhangi bir matrisin tersinin devriginin tersi kendisine esittir A T displaystyle A T seklinde yazim yukardaki esitlikteki sag veya sol taraftaki terimlerden herhangi birini ifade etmek icin kullanilir Eger A displaystyle A kare bir matris ise bu matrisin ozdegerleri ile devriklerinin ozdegerleri birbirine esittir Kaynakca Terimler org sayfasinda matrisin devrigi teriminin tanimi Erisim tarihi 25 Ocak 2025 Terimler org sayfasinda devrik matris teriminin tanimi Erisim tarihi 25 Ocak 2025
 Azərbaycanca
Azərbaycanca Deutsch
Deutsch 日本語
日本語 Lietuvos
Lietuvos සිංහල
සිංහල Türkçe
Türkçe Українська
Українська United State
United State
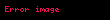

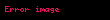
![{\displaystyle [A^{T}]_{ij}=[A]_{ji}}](https://www.wikipedia.tr-tr.nina.az/image/aHR0cHM6Ly93d3cud2lraXBlZGlhLnRyLXRyLm5pbmEuYXovaW1hZ2UvYUhSMGNITTZMeTkzYVd0cGJXVmthV0V1YjNKbkwyRndhUzl5WlhOMFgzWXhMMjFsWkdsaEwyMWhkR2d2Y21WdVpHVnlMM04yWnk4MU1HRXdOVE13Tm1Oa01ESXhPREkwWVRFMVl6Y3pPVGszWm1FNU9EUmtNV1V3WlRrMk5EUTEuc3Zn.svg)
















