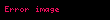Paramanyetik bir malzemede, malzemenin mıknatıslanması genel olarak uygulanan manyetik alanla orantılıdır. Fakat eğer malzeme ısıtılırsa, bu oran düşer: Belirli bir sıcaklığa kadar, mıknatıslanma sıcaklıkla ters orantılıdır. Bu kavram “Curie Yasası” tarafından kapsanmaktadır:
Formülde:
- :En son elde edilen mıknatıslanma
- :Manyetik Alan, birimi
- :Salt Sıcaklık, Birimi kelvin
- :Malzemeye özgü .
Bu ilişki Pierre Curie tarafından deneysel olarak; sonuçları, doğru tahmin edilmiş modellere uydurarak keşfedilmiştir. Bu yasa sadece yüksek sıcaklıklar ya da zayıf manyetik alanlar için geçerlidir. Aşağıdaki derivasyonların da gösterdiği gibi, mıknatıslanma düşük sıcaklığın karşıt limiti veya güçlü bir manyetik alanda doygunluğa ulaşır.
Kuantum Mekaniği ile Derivasyonu

Paramanyetik mıknatısların basit matematik modellemeri, birbirleriyle etkileşmeyen parçacıkların derlenmesine odaklanır. Her parçacığın 
İki Durumlu parçacıklar(Spin1-2)
İşlemi basitleştirmek için, 2 durumlu parçacıklarla çalışacağız: bu sayede parçacık ya manyetik momente destek olacak ya da ona karşı çıkacak. Bu sayede manyetik momentin mümkün olan değerleri 

Ve
Ne zaman birisi paramanyetik mıknatısın, mıknatıslanmasına baksa, ilk baktığı şey parçacığın dıştaki manyetik alanla kendisini aynı yöne getirip getiremediğidir. Diğer bir deyişle, mıknatıslanmanın(
Burada konfigürasyonun olasılığı kendisinin verilir ve 
Bu sayede, bu basit durumda elimizde şu denklem kalır.
Bu tek bir parçacığın mıknatıslanmasıdır. Katı maddenin toplam mıknatıslanması aşağıdaki denklemle bulunur.
Yukarıdaki formül olarak bilinmektedir.
Pierre Curie, bu kanununun, deneyinde kullandığı yüksek sıcaklık ve düşük manyetik alanlar için de uygulanabilen yaklaşımını bulmuştur. Şimdi yüksek sıcaklık (

Zaman zaman buna Curie rejimi de denmektedir. Şunu da biliyoruz ki, şayet 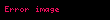
Böylece
Denklemden çıkan : 


Genel Durum
Parçacığın rastgele bir dönüşü(rastegel bir spin numarası) olduğunda, formül biraz daha karmaşık bir hal alır. Düşük manyetik alanlar veya yüksek sıcaklıklarda, dönüş(spin) Curie yasasını
İfadesi ile takip eder. Buarada 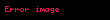


Klasik istatistiksel mekanikle olan çıkarım
Paramagnetonların(basit şekilde, paramanyetizmaya sebep olan parçacıklar), klasik bir biçimde, serbestçe dönen manyetik momentler olduğunu düşünürsek, alternatif bir yaklaşım da mümkündür. Böyle bir durumda, bu parçacıkların pozisyonlarını açılarıyla belirlenebilir ve bir tanesinin enerjisi aşağıdaki formülle bulunur.
: Manyetik Momentle, manyetik alan alan arasındaki; z koordinatını gösteriyor kabul edilen açı
Buna bağlı ayrılım fonksiyonu:
Değerin açıya(

Şimdi, mıknatıslanmanın z koordinatındaki elemanının beklenen değeri(diğerleri açı üzerinden alınan integral itibarıyla, beklendiği gibi sıfıra gidecek) aşağıdaki formüldeki gibidir.
İşlemi basitleştirmek için, üstteki formül 
(Bu yaklaşım üstteki model için de kullabilir, fakat işlem zaten basit olduğundan çok faydalı değil.)
Çıkarımı devam ettirirsek:
: :
Bu fonksiyon küçük 


Uygulamaları
Bu kavram, manyetik termometrelerin, ki çok düşük sıcaklıkların ölçümü bu aletlerle yapılmaktadır, temelini oluşturmaktadır.
Ayrıca bakınız
Kaynakça
wikipedia, wiki, viki, vikipedia, oku, kitap, kütüphane, kütübhane, ara, ara bul, bul, herşey, ne arasanız burada,hikayeler, makale, kitaplar, öğren, wiki, bilgi, tarih, yukle, izle, telefon için, turk, türk, türkçe, turkce, nasıl yapılır, ne demek, nasıl, yapmak, yapılır, indir, ücretsiz, ücretsiz indir, bedava, bedava indir, mp3, video, mp4, 3gp, jpg, jpeg, gif, png, resim, müzik, şarkı, film, film, oyun, oyunlar, mobil, cep telefonu, telefon, android, ios, apple, samsung, iphone, xiomi, xiaomi, redmi, honor, oppo, nokia, sonya, mi, pc, web, computer, bilgisayar
Paramanyetik bir malzemede malzemenin miknatislanmasi genel olarak uygulanan manyetik alanla orantilidir Fakat eger malzeme isitilirsa bu oran duser Belirli bir sicakliga kadar miknatislanma sicaklikla ters orantilidir Bu kavram Curie Yasasi tarafindan kapsanmaktadir M C BT displaystyle mathbf M C cdot frac mathbf B T Formulde M displaystyle mathbf M En son elde edilen miknatislanma B displaystyle mathbf B Manyetik Alan birimi T displaystyle T Salt Sicaklik Birimi kelvin C displaystyle C Malzemeye ozgu Bu iliski Pierre Curie tarafindan deneysel olarak sonuclari dogru tahmin edilmis modellere uydurarak kesfedilmistir Bu yasa sadece yuksek sicakliklar ya da zayif manyetik alanlar icin gecerlidir Asagidaki derivasyonlarin da gosterdigi gibi miknatislanma dusuk sicakligin karsit limiti veya guclu bir manyetik alanda doygunluga ulasir Kuantum Mekanigi ile DerivasyonuParamanyetik malzemenin miknatislanmasinin sicakligin tersiyle gosterilmis fonksiyonu Paramanyetik miknatislarin basit matematik modellemeri birbirleriyle etkilesmeyen parcaciklarin derlenmesine odaklanir Her parcacigin m displaystyle vec mu ile kazandigi bir manyetik momenti vardir Manyetik alan icerisindeki manyetik momentin enerjisi asagidaki formuldeki gibidir E m B displaystyle E vec mu cdot vec B Iki Durumlu parcaciklar Spin1 2 Islemi basitlestirmek icin 2 durumlu parcaciklarla calisacagiz bu sayede parcacik ya manyetik momente destek olacak ya da ona karsi cikacak Bu sayede manyetik momentin mumkun olan degerleri m displaystyle mu and m displaystyle mu dur Boyleyken parcacigin sadece 2 olasi enerjisi olabilir E0 mB displaystyle E 0 mu B Ve E1 mB displaystyle E 1 mu B Ne zaman birisi paramanyetik miknatisin miknatislanmasina baksa ilk baktigi sey parcacigin distaki manyetik alanla kendisini ayni yone getirip getiremedigidir Diger bir deyisle miknatislanmanin m displaystyle mu beklenen degerine bakilir m mP m m P m 1Z memBb me mBb 2mZsinh mBb displaystyle left langle mu right rangle mu P left mu right mu P left mu right 1 over Z left mu e mu B beta mu e mu B beta right 2 mu over Z sinh mu B beta Burada konfigurasyonun olasiligi kendisinin verilir ve Z displaystyle Z ise bize olasiliklar icin gerekli olan duzgeleme katsayisini temin eder Bu sayede tum olasiliklarim toplami bir edebilir Bir parcacik icin ayrilim fonksiyonu Z n 0 1e Enb emBb e mBb 2cosh mBb displaystyle Z sum n 0 1 e E n beta e mu B beta e mu B beta 2 cosh left mu B beta right Bu sayede bu basit durumda elimizde su denklem kalir m mtanh mBb displaystyle left langle mu right rangle mu tanh left mu B beta right Bu tek bir parcacigin miknatislanmasidir Kati maddenin toplam miknatislanmasi asagidaki denklemle bulunur M N m Nmtanh mBkT displaystyle M N left langle mu right rangle N mu tanh left mu B over kT right Yukaridaki formul olarak bilinmektedir Pierre Curie bu kanununun deneyinde kullandigi yuksek sicaklik ve dusuk manyetik alanlar icin de uygulanabilen yaklasimini bulmustur Simdi yuksek sicaklik T displaystyle T ve dusuk manyetik alanda B displaystyle B miknatislanmanin durumuna bakalim Sicaklik artip manyetik alan azaldikca hiperbolik tanjantin argumani azalmaktadir Diger bir sekilde gormek icin mBkT 1 displaystyle left mu B over kT right ll 1 Zaman zaman buna Curie rejimi de denmektedir Sunu da biliyoruz ki sayet x 1 displaystyle x ll 1 o zaman tanh x x displaystyle tanh x approx x Boylece M T Nm2kBT displaystyle mathbf M T rightarrow infty N mu 2 over k mathbf B over T Denklemden cikan C Nm2 k displaystyle C N mu 2 k Zit durumdaysa dusuk sicaklik buyuk manyetik alan M displaystyle M Nm displaystyle N mu nun maksimum degerine yaklasir ki bu da tum parcaciklarin uygulanan manyetik alanla ayni hizaya girmesi demek Genel Durum Parcacigin rastgele bir donusu rastegel bir spin numarasi oldugunda formul biraz daha karmasik bir hal alir Dusuk manyetik alanlar veya yuksek sicakliklarda donus spin Curie yasasini C mB23kBNg2J J 1 displaystyle C frac mu B 2 3k B Ng 2 J J 1 Ifadesi ile takip eder Buarada J displaystyle J ve g displaystyle g is donusun g faktorunu gostermektedir Oyle ki m gJmB displaystyle mu gJ mu B manyetik momenttir Bu daha genel formulu ve onun cikarilisi icin yuksek manyetik alan ve dusuk sicakligi da iceren haliyle makalesine bakiniz Donus sonsuza yaklastikca miknatislanma formulu bir sonraki kisimda hesaplanan klasik degere yaklasmaktadir Klasik istatistiksel mekanikle olan cikarimParamagnetonlarin basit sekilde paramanyetizmaya sebep olan parcaciklar klasik bir bicimde serbestce donen manyetik momentler oldugunu dusunursek alternatif bir yaklasim da mumkundur Boyle bir durumda bu parcaciklarin pozisyonlarini acilariyla belirlenebilir ve bir tanesinin enerjisi asagidaki formulle bulunur E mBcos 8 displaystyle E mu B cos theta 8 displaystyle theta Manyetik Momentle manyetik alan alan arasindaki z koordinatini gosteriyor kabul edilen aci Buna bagli ayrilim fonksiyonu Z 02pdϕ 0pd8sin 8exp mBbcos 8 displaystyle Z int 0 2 pi d phi int 0 pi d theta sin theta exp mu B beta cos theta Degerin aciya ϕ displaystyle phi bagli olmadigi gozukuyor Bu sayede y cos 8 displaystyle y cos theta degisimini yapabiliriz Z 2p 11dyexp mBby 2pexp mBb exp mBb mBb 4psinh mBb mBb displaystyle Z 2 pi int 1 1 dy exp mu B beta y 2 pi exp mu B beta exp mu B beta over mu B beta 4 pi sinh mu B beta over mu B beta Simdi miknatislanmanin z koordinatindaki elemaninin beklenen degeri digerleri aci uzerinden alinan integral itibariyla beklendigi gibi sifira gidecek asagidaki formuldeki gibidir mz 1Z 02pdϕ 0pd8sin 8exp mBbcos 8 mcos 8 displaystyle left langle mu z right rangle 1 over Z int 0 2 pi d phi int 0 pi d theta sin theta exp mu B beta cos theta left mu cos theta right Islemi basitlestirmek icin ustteki formul Z displaystyle Z nin turevi seklinde yazilabilir mz 1ZB bZ displaystyle left langle mu z right rangle 1 over ZB partial beta Z Bu yaklasim ustteki model icin de kullabilir fakat islem zaten basit oldugundan cok faydali degil Cikarimi devam ettirirsek mz mL mBb displaystyle left langle mu z right rangle mu L mu B beta L displaystyle L L x coth x 1x displaystyle L x coth x 1 over x Bu fonksiyon kucuk x displaystyle x degerleri icin tekilmis gibi gozukebilir fakat degildir Cunku formuldeki tekil ifadeler birbirini goturur Aslinda kucuk degerler icin bunun davranisi L x x 3 displaystyle L x approx x 3 dir Boylece Curie siniri halen gecerli olmakla birlikte Curie katsayisi 3 kat daha kucuktur Benzer sekilde fonksiyon argumaninin yuksek degerleri icin 1 displaystyle 1 de doygunluga ulasir Ters sinir da benzer bir sekilde duzelir UygulamalariBu kavram manyetik termometrelerin ki cok dusuk sicakliklarin olcumu bu aletlerle yapilmaktadir temelini olusturmaktadir Ayrica bakinizKaynakca Kittel Charles 2005 Introduction to Solid State Physics 8th Edition Wiley ss 304 ISBN 0 471 41526 X
 Azərbaycanca
Azərbaycanca Deutsch
Deutsch 日本語
日本語 Lietuvos
Lietuvos සිංහල
සිංහල Türkçe
Türkçe Українська
Українська United State
United State