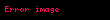Brocard noktaları, geometride bir üçgen içinde yer alan özel noktalardır. Fransız matematikçi Henri Brocard'ın çalışmalarından dolayı bu adı almıştır.

Tanım
Kenarları 






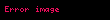

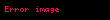





Bu 



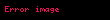






denklemi bu nokta için de geçerlidir. Dikkat çekici biçimde, bu ikinci Brocard noktası ile birinci Brocard noktası aynı Brocard açısına sahiptir. Yani
ve
birbirine eşittir.
İki Brocard noktası arasında yakın ilişki vardır; aslında ikisi arasındaki fark 



Elde edilmesi
Brocard noktalarını oluşturmanın en iyi yolu için şöyle denebilir. Verilecek örnekte sadece birinci Brocard noktası ele alınacak ancak ikinci Brocard noktasını bulmak buna çok benzerdir.













İkinci Brocard noktası aynı yöntemle tespit edilebilir.
Kaynakça
- Akopyan, A. V.; Zaslavsky, A. A. (2007), Geometry of Conics, Mathematical World, 26, American Mathematical Society, ss. 48-52, ISBN .
- Honsberger, Ross (1995), "Chapter 10. The Brocard Points", Episodes in Nineteenth and Twentieth Century Euclidean Geometry, Washington, D.C.: The Mathematical Association of America.
Dış bağlantılar
- Eric W. Weisstein, Üçüncü Brocard Noktası (MathWorld)
wikipedia, wiki, viki, vikipedia, oku, kitap, kütüphane, kütübhane, ara, ara bul, bul, herşey, ne arasanız burada,hikayeler, makale, kitaplar, öğren, wiki, bilgi, tarih, yukle, izle, telefon için, turk, türk, türkçe, turkce, nasıl yapılır, ne demek, nasıl, yapmak, yapılır, indir, ücretsiz, ücretsiz indir, bedava, bedava indir, mp3, video, mp4, 3gp, jpg, jpeg, gif, png, resim, müzik, şarkı, film, film, oyun, oyunlar, mobil, cep telefonu, telefon, android, ios, apple, samsung, iphone, xiomi, xiaomi, redmi, honor, oppo, nokia, sonya, mi, pc, web, computer, bilgisayar
Brocard noktalari geometride bir ucgen icinde yer alan ozel noktalardir Fransiz matematikci Henri Brocard in calismalarindan dolayi bu adi almistir Uc cemberin kesisim noktasinda olusturulmus bir ucgene ait Brocard noktasi TanimKenarlari a displaystyle a b displaystyle b ve c displaystyle c koseleri saat yonunun tersine dogru A displaystyle A B displaystyle B ve C displaystyle C olarak adlandirilmis bir ABC displaystyle triangle ABC ucgeninde AP displaystyle AP BP displaystyle BP ve CP displaystyle CP sirasiyla c displaystyle c a displaystyle a ve b displaystyle b kenarlariyla esit w displaystyle omega acisi yapacak sekilde bir P displaystyle P noktasi bulunur PAB PBC PCA displaystyle angle PAB angle PBC angle PCA Bu P displaystyle P noktasina ABC displaystyle triangle ABC ucgeninin birinci Brocard noktasi ve w displaystyle omega acisina ucgenin Brocard acisi denir Bu aci su denklemi saglar cot w cot a cot b cot g displaystyle cot omega cot alpha cot beta cot gamma ABC displaystyle triangle ABC ucgeninde AQ displaystyle AQ BQ displaystyle BQ ve CQ displaystyle CQ dogru parcalarinin sirasiyla b displaystyle b c displaystyle c ve a displaystyle a kenarlariyla esit aci yapmasi sartini saglayan bir Q displaystyle Q ikinci Brocard noktasi bulunur Diger bir deyisle QCB QBA QAC displaystyle angle QCB angle QBA angle QAC denklemi bu nokta icin de gecerlidir Dikkat cekici bicimde bu ikinci Brocard noktasi ile birinci Brocard noktasi ayni Brocard acisina sahiptir Yani PBC PCA PAB displaystyle angle PBC angle PCA angle PAB ve QCB QBA QAC displaystyle angle QCB angle QBA angle QAC birbirine esittir Iki Brocard noktasi arasinda yakin iliski vardir aslinda ikisi arasindaki fark ABC displaystyle triangle ABC ucgeninin acilarinin hangi sirayla secildigine baglidir Ornek verilirse ABC displaystyle triangle ABC ucgeninin birinci Brocard noktasi ACB displaystyle triangle ACB ucgeninin ikinci Brocard noktasidir ABC displaystyle triangle ABC ucgeninin iki Brocard noktasi birbirinin Elde edilmesiBrocard noktalarini olusturmanin en iyi yolu icin soyle denebilir Verilecek ornekte sadece birinci Brocard noktasi ele alinacak ancak ikinci Brocard noktasini bulmak buna cok benzerdir A displaystyle A ile B displaystyle B noktalarindan gecen ucgenin BC displaystyle BC kenarina teget bir cember bu cemberin merkezi AB displaystyle AB nin orta dikmesi ile B displaystyle B noktasindan BC displaystyle BC ye dik olarak cizilecek dogrunun kesisim noktasi olacaktir olusturulur Simetrik olarak B displaystyle B ile C displaystyle C noktalarindan gecen AC displaystyle AC kenarina teget ve A displaystyle A ile C displaystyle C noktalarindan gecen AB displaystyle AB kenarina teget cemberler cizilir Bu uc cemberin ortak tek noktasi ABC displaystyle triangle ABC ucgeninin birinci Brocard noktasidir Ikinci Brocard noktasi ayni yontemle tespit edilebilir KaynakcaAkopyan A V Zaslavsky A A 2007 Geometry of Conics Mathematical World 26 American Mathematical Society ss 48 52 ISBN 978 08218 4323 9 Honsberger Ross 1995 Chapter 10 The Brocard Points Episodes in Nineteenth and Twentieth Century Euclidean Geometry Washington D C The Mathematical Association of America Dis baglantilarEric W Weisstein Ucuncu Brocard Noktasi MathWorld
 Azərbaycanca
Azərbaycanca Deutsch
Deutsch 日本語
日本語 Lietuvos
Lietuvos සිංහල
සිංහල Türkçe
Türkçe Українська
Українська United State
United State