Geometride, Brahmagupta teoremi, eğer bir kirişler dörtgeni ortodiyagonal ise (yani, dik köşegenlere sahipse), o zaman köşegenlerin kesişme noktasından bir kenara çizilen dikmenin karşı kenarı daima ikiye böldüğünü belirtir. Adını Hint matematikçi Brahmagupta'dan (598-668) almıştır.

Teoremin açıklaması
Daha spesifik olarak, 












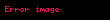



Teoremin ispatı


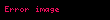


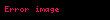






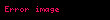










Ayrıca bakınız
- Kirişler dörtgeninin alanı için Brahmagupta formülü
Kaynakça
- ^ a b Bradley, Michael (2006). The birth of mathematics : ancient times to 1300. New York: Infobase Publishing. ss. 70, 85. ISBN . OCLC 62152830.
- ^ ; Greitzer, Samuel L. (1967). Geometry Revisited (PDF). 19. Washington, DC: Math. Assoc. Amer. s. 59. ISBN . 23 Ocak 2021 tarihinde kaynağından (PDF). Erişim tarihi: 4 Şubat 2021.
Dış bağlantılar ve ilave okumalar
- Brahmagupta teoremi 17 Şubat 2011 tarihinde Wayback Machine sitesinde . @ Proofwiki
- Brahmagupta Teoremi 22 Eylül 2020 tarihinde Wayback Machine sitesinde . @ Cut-the-Knot
- Eric W. Weisstein, Brahmagupta's theorem (MathWorld)
- Murthy, M. N. (2019). Brahmagupta’s theorem. At Right Angles, (5), 27.
- Kaye, G. R. (1919). Indian mathematics. Isis, 2(2), ss. 326-356.
- Dvorožňák, Marek & Pech, Pavel. (2009), Brahmagupta’s Theorem Automatic Computer Proof
- Askey R. (2010) Completing Brahmagupta’s Extension of Ptolemy’s Theorem. In: Alladi K., Klauder J., Rao C. (eds) The Legacy of Alladi Ramakrishnan in the Mathematical Sciences. Springer, New York, NY. https://doi.org/10.1007/978-1-4419-6263-8_11
- Dashrath Kumar & Dr. Mrityunjay JhaA, (2019), Critical Study of Brahmagupta’s Theorems on Cyclic Quadrilateral 10 Ekim 2020 tarihinde Wayback Machine sitesinde ., JETIR, March 2019, Volume 6, Issue 3, ISSN 2349-5162, ss. 383-384
- Richeson, A. (1930). An Extension of Brahmagupta's Theorem. American Journal of Mathematics, 52(2), ss. 425-438. doi:10.2307/2370695
wikipedia, wiki, viki, vikipedia, oku, kitap, kütüphane, kütübhane, ara, ara bul, bul, herşey, ne arasanız burada,hikayeler, makale, kitaplar, öğren, wiki, bilgi, tarih, yukle, izle, telefon için, turk, türk, türkçe, turkce, nasıl yapılır, ne demek, nasıl, yapmak, yapılır, indir, ücretsiz, ücretsiz indir, bedava, bedava indir, mp3, video, mp4, 3gp, jpg, jpeg, gif, png, resim, müzik, şarkı, film, film, oyun, oyunlar, mobil, cep telefonu, telefon, android, ios, apple, samsung, iphone, xiomi, xiaomi, redmi, honor, oppo, nokia, sonya, mi, pc, web, computer, bilgisayar
Geometride Brahmagupta teoremi eger bir kirisler dortgeni ortodiyagonal ise yani dik kosegenlere sahipse o zaman kosegenlerin kesisme noktasindan bir kenara cizilen dikmenin karsi kenari daima ikiye boldugunu belirtir Adini Hint matematikci Brahmagupta dan 598 668 almistir BD AC EF BC displaystyle overline BD perp overline AC overline EF perp overline BC AF FD displaystyle Rightarrow overline AF overline FD Teoremin aciklamasiDaha spesifik olarak A displaystyle A B displaystyle B C displaystyle C ve D displaystyle D AC displaystyle AC ve BD displaystyle BD dogrularinin dik olacagi sekilde bir daire uzerinde dort nokta olsun AC displaystyle AC ve BD displaystyle BD nin kesisme noktasini M displaystyle M ile gosterilsin M displaystyle M den BC displaystyle BC dogrusuna dik cizilsin ve E displaystyle E kesisme noktasina gelsin F displaystyle F EM displaystyle EM dogrusu ile AD displaystyle AD kenarinin kesisim noktasi olsun Daha sonra teorem F displaystyle F nin AD displaystyle AD dogru parcasinin orta noktasi oldugunu belirtir Teoremin ispatiTeoremin kaniti AF FD displaystyle AF FD oldugunu kanitlamamiz gerekiyor Biz AF displaystyle AF ve FD displaystyle FD nin aslinda FM displaystyle FM ye esit olduklarini ispat edecegiz AF FM displaystyle AF FM oldugunu kanitlamak icin once FAM displaystyle angle FAM ve CBM displaystyle angle CBM acilarinin esit olduguna dikkat edin cunku bunlar dairenin ayni yayini goren cevre acilardir Ayrica CBM displaystyle angle CBM ve CME displaystyle angle CME acilarinin her ikisi de BCM displaystyle angle BCM acisina tamamlayicidir yani toplamlari 90 ye esittir ve bu nedenle her iki aci esittirler Son olarak CME displaystyle angle CME ve FMA displaystyle angle FMA acilari aynidir Dolayisiyla AFM displaystyle triangle AFM bir ikizkenar ucgendir ve dolayisiyla AF displaystyle AF ve FM displaystyle FM kenarlari esittir FD FM displaystyle FD FM nin benzer sekilde gittiginin kaniti FDM displaystyle angle FDM BCM displaystyle angle BCM BME displaystyle angle BME ve DMF displaystyle angle DMF acilarinin tumu esittir bu nedenle DFM displaystyle triangle DFM bir ikizkenar ucgendir dolayisiyla FD FM displaystyle FD FM dir Buradan teoremin iddia ettigi gibi AF FD displaystyle AF FD oldugu gorulebilir Ayrica bakinizKirisler dortgeninin alani icin Brahmagupta formuluKaynakca a b Bradley Michael 2006 The birth of mathematics ancient times to 1300 New York Infobase Publishing ss 70 85 ISBN 0 8160 5423 1 OCLC 62152830 Greitzer Samuel L 1967 Geometry Revisited PDF 19 Washington DC Math Assoc Amer s 59 ISBN 0 88385 619 0 23 Ocak 2021 tarihinde kaynagindan PDF Erisim tarihi 4 Subat 2021 Dis baglantilar ve ilave okumalarBrahmagupta teoremi 17 Subat 2011 tarihinde Wayback Machine sitesinde Proofwiki Brahmagupta Teoremi 22 Eylul 2020 tarihinde Wayback Machine sitesinde Cut the Knot Eric W Weisstein Brahmagupta s theorem MathWorld Murthy M N 2019 Brahmagupta s theorem At Right Angles 5 27 Kaye G R 1919 Indian mathematics Isis 2 2 ss 326 356 Dvoroznak Marek amp Pech Pavel 2009 Brahmagupta s Theorem Automatic Computer Proof Askey R 2010 Completing Brahmagupta s Extension of Ptolemy s Theorem In Alladi K Klauder J Rao C eds The Legacy of Alladi Ramakrishnan in the Mathematical Sciences Springer New York NY https doi org 10 1007 978 1 4419 6263 8 11 Dashrath Kumar amp Dr Mrityunjay JhaA 2019 Critical Study of Brahmagupta s Theorems on Cyclic Quadrilateral 10 Ekim 2020 tarihinde Wayback Machine sitesinde JETIR March 2019 Volume 6 Issue 3 ISSN 2349 5162 ss 383 384 Richeson A 1930 An Extension of Brahmagupta s Theorem American Journal of Mathematics 52 2 ss 425 438 doi 10 2307 2370695
 Azərbaycanca
Azərbaycanca Deutsch
Deutsch 日本語
日本語 Lietuvos
Lietuvos සිංහල
සිංහල Türkçe
Türkçe Українська
Українська United State
United State

