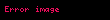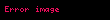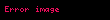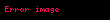Belirsiz, matematikte bize verildiği haliyle değerini belirleyemediğimiz ifadelere denir. Daha önce tanımlanmadığı için bir anlam ifade etmeyen tanımsız ifadelere kıyasla belirsiz ifadeler, eldeki verinin daha dikkatli incelenmesi sonucu bir değere sahip olurlar. Özellikle fonksiyonların limiti konusunda karşımıza çıkan bu durum, kötü bir yazım tercihinden dolayı çok kafa karışıklığına yol açmaktadır. Örneğin '0/0 belirsizliği' adındaki durum, aslında limitleri sıfıra giden iki fonksiyonun oranı ile ilgilidir, 0 sayısının 0 ile bölümü ile ilgili değil. Eğer bir noktada hem f(x), hem g(x) fonksiyonunun limiti sıfıra gidiyorsa, bu iki fonksiyonun oranının limiti '0/0 tipindeki belirsizlik' olarak geçer, sayısal değeri bu fonksiyonların ne olduğuna göre değişir. Ancak fonksiyonlar belirlendikten sonra oranlarının limiti de belirlenmiş olur.
belirsizliği
belirsizliği
belirsizliği
belirsizliği
belirsizliği
belirsizliği
belirsizliği
ve belirsizliği
belirsizliği
Bir sayının sonsuza bölümü
wikipedia, wiki, viki, vikipedia, oku, kitap, kütüphane, kütübhane, ara, ara bul, bul, herşey, ne arasanız burada,hikayeler, makale, kitaplar, öğren, wiki, bilgi, tarih, yukle, izle, telefon için, turk, türk, türkçe, turkce, nasıl yapılır, ne demek, nasıl, yapmak, yapılır, indir, ücretsiz, ücretsiz indir, bedava, bedava indir, mp3, video, mp4, 3gp, jpg, jpeg, gif, png, resim, müzik, şarkı, film, film, oyun, oyunlar, mobil, cep telefonu, telefon, android, ios, apple, samsung, iphone, xiomi, xiaomi, redmi, honor, oppo, nokia, sonya, mi, pc, web, computer, bilgisayar
Belirsiz matematikte bize verildigi haliyle degerini belirleyemedigimiz ifadelere denir Daha once tanimlanmadigi icin bir anlam ifade etmeyen tanimsiz ifadelere kiyasla belirsiz ifadeler eldeki verinin daha dikkatli incelenmesi sonucu bir degere sahip olurlar Ozellikle fonksiyonlarin limiti konusunda karsimiza cikan bu durum kotu bir yazim tercihinden dolayi cok kafa karisikligina yol acmaktadir Ornegin 0 0 belirsizligi adindaki durum aslinda limitleri sifira giden iki fonksiyonun orani ile ilgilidir 0 sayisinin 0 ile bolumu ile ilgili degil Eger bir noktada hem f x hem g x fonksiyonunun limiti sifira gidiyorsa bu iki fonksiyonun oraninin limiti 0 0 tipindeki belirsizlik olarak gecer sayisal degeri bu fonksiyonlarin ne olduguna gore degisir Ancak fonksiyonlar belirlendikten sonra oranlarinin limiti de belirlenmis olur 00 displaystyle 0 0 belirsizligi 0 displaystyle infty 0 belirsizligi1 displaystyle 1 infty belirsizligi displaystyle infty infty belirsizligi displaystyle infty infty belirsizligi0 displaystyle 0 times infty belirsizligi 0 displaystyle infty times 0 belirsizligi displaystyle infty over infty ve displaystyle infty infty belirsizligi00 displaystyle 0 over 0 belirsizligiBir sayinin sonsuza bolumu
 Azərbaycanca
Azərbaycanca Deutsch
Deutsch 日本語
日本語 Lietuvos
Lietuvos සිංහල
සිංහල Türkçe
Türkçe Українська
Українська United State
United State