Bağıntı

Matematikte iki kümenin kartezyen çarpımının herhangi bir alt kümesi bağıntı olarak tanımlanır. Bir kümedeki bir öğeyi başka bir kümedeki bir öğeye götürür. Yâni iki öğe arasında bir bağ kurar. Örneğin, göndermeler tek yönlü bir bağıntıdır.

Tanım

A ve B herhangi iki küme olsun. 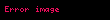${\displaystyle A\times B}$'nin herhangi bir altkümesine bağıntı denir:

(2)İki ya da daha çok şey arasındaki karşılıklı ilişki, ilinti.

Eşyayı, kavramları ya da tasarımları birlik, bağlılık, birliktelik gibi durumlarda toplayan görünüş ya da nitelik, görelik, °izafiyet, °rölativite.

${\displaystyle \beta =\{(a,b)\,|\,a\in A,\,b\in B\}\subseteq A\times B}$

burada a ile b öğeleri arasında bir bağ vardır. Dikkat edilirse bir bağıntı boş olabilir. Çünkü kümedeki öğelerin varlığından söz edilmiyor. Eğer 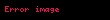${\displaystyle \exists }$ simgesi olsaydı o zaman öğelerin varlığı zorunlu olurdu. Boşküme de kartezyen uzayın bir altkümesi olduğu için boş bağıntı mümkündür.

Daha genel olarak, birbirinden farklı olması gerekmeyen n küme (${\displaystyle A_{1},A_{2},...,A_{n}}$) arasındaki n 'li bağıntı (${\displaystyle \beta }$), bu kümelerin kartezyen çarpımının herhangi bir alt kümesidir.

${\displaystyle \beta ={(a_{1},\cdots ,a_{n})\,|\,a_{i}\in A_{i}}\subseteq A_{1}\times A_{2}\times \cdots \times A_{n}}$

n, iki ise olarak adlandırılır.

Örnekler

Evlilik ilişkisi

A={Ayşe, Fatma, Esra, Ali, Veli, Ahmet, Mehmet}

A ile A arasındaki hayali bir evlilik ilişki (E) aşağıdaki gibi olabilir:

E={(Ayşe, Ali), (Ali, Ayşe), (Esra, Mehmet), (Mehmet, Esra)}

Buna göre A kümesinin elemanlarından, Ayşe ve Ali, Esra ve Mehmet evlidir.

Yaşça büyüklük ilişkisi

Bütün ilişkiler simetrik olmak zorunda değildir. Örneğin K kümesinden, yaşça büyüklük ilişkisi (B) şöyle olabilir.

K={Ayşe, Fatma, Esra}

B={(Fatma, Ayşe), (Fatma, Esra), (Esra, Ayşe)}

Bu ilişkiye göre yaş sıralaması büyükten küçüğe Fatma, Esra, Ayşe şeklindedir.

Bağıntı çeşitleri

1. Denklik bağıntısı: Bağıntıda yansıma, simetri ve geçişme özelliği olan bağıntı.
2. : Bağıntıda yansıma, ters simetri ve geçişme özelliği olan bağıntı.

Kaynakça

• Bağıntı nedir? 6 Mayıs 2021 tarihinde Wayback Machine sitesinde .

1. ^ "Sıralama bağıntısı". 6 Mayıs 2021 tarihinde kaynağından . Erişim tarihi: 6 Mayıs 2021. 

Ayrıca bakınız

• İlişkisel cebir
• Mantık bağlacı
• Mantık cümlesi
• Gönderme (Fonksiyon)
• Küme