Geometride Barrow eşitsizliği, bir üçgen içindeki rastgele bir nokta alındığında, bu nokta ile üçgenin köşeleri ve üçgenin kenarlarındaki belirli noktalar arasındaki mesafeleri ilişkilendiren bir eşitsizliktir. Adını Amerikalı bir matematikçi olan 'dan almıştır.

Açıklama













Eşitlik sadece eşkenar üçgen durumunda sağlanır ve bu durumda 
İspat










,
,
.
Aritmetik Ortalama-Geometrik Ortalama eşitsizliği ve yukarıdaki sonuçla, bu şu anlama gelir:
İstenen ifade ispatlanmış olur.
Genelleştirme
Barrow eşitsizliği dışbükey çokgenlere kadar genişletilebilir. Köşeleri 




Burada 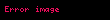
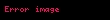

Tarihçe


Barrow eşitsizliği, 



Daha basit bir kanıt daha sonra tarafından verildi.
Ayrıca bakınız
- Geometride Euler teoremi
Kaynakça
- ^ a b c Erdős, Paul; ; (1937), "Solution to problem 3740", , 44 (4), ss. 252-254, doi:10.2307/2300713, JSTOR 2300713.
- ^ M. Dinca: "A Simple Proof of the Erdös-Mordell Inequality" 13 Kasım 2020 tarihinde Wayback Machine sitesinde .. In: Articole si Note Matematice, 2009
- ^ Hans-Christof Lenhard: "Verallgemeinerung und Verschärfung der Erdös-Mordellschen Ungleichung für Polygone". In: Archiv für Mathematische Logik und Grundlagenforschung, Band 12, S. 311–314, doi:10.1007/BF01650566 (Almanca).
- ^ (1961), "New inequalities for a triangle and an internal point", , cilt 53, ss. 157-163, doi:10.1007/BF02417793, MR 0124774
- ^ (1962), "On geometric problems of Erdös and Oppenheim", , 46 (357), ss. 213-215, JSTOR 3614019.
Dış bağlantılar
- Barrow's Inequality 4 Haziran 2018 tarihinde Wayback Machine sitesinde . @ Wolfram Demonstrations Project
Konuyla ilgili yayınlar
- Malesevic, Branko & Petrovic, Maja. (2014). Barrow's Inequality and Signed Angle Bisectors. Journal of Mathematical Inequalities. 10.7153/jmi-08-40., Makale 10 Kasım 2020 tarihinde Wayback Machine sitesinde . veya Makale 10 Ağustos 2017 tarihinde Wayback Machine sitesinde .
- Liu, Jian. (2016). Refinements of the Erdös-Mordell inequality, Barrow’s inequality, and Oppenheim’s inequality. Journal of Inequalities and Applications. 2016. 10.1186/s13660-015-0947-2., Makale
- Liu, Jian. (2019). New Refinements of the Erdös–Mordell Inequality and Barrow’s Inequality, https://doi.org/10.3390/math7080726, Makale
wikipedia, wiki, viki, vikipedia, oku, kitap, kütüphane, kütübhane, ara, ara bul, bul, herşey, ne arasanız burada,hikayeler, makale, kitaplar, öğren, wiki, bilgi, tarih, yukle, izle, telefon için, turk, türk, türkçe, turkce, nasıl yapılır, ne demek, nasıl, yapmak, yapılır, indir, ücretsiz, ücretsiz indir, bedava, bedava indir, mp3, video, mp4, 3gp, jpg, jpeg, gif, png, resim, müzik, şarkı, film, film, oyun, oyunlar, mobil, cep telefonu, telefon, android, ios, apple, samsung, iphone, xiomi, xiaomi, redmi, honor, oppo, nokia, sonya, mi, pc, web, computer, bilgisayar
Geometride Barrow esitsizligi bir ucgen icindeki rastgele bir nokta alindiginda bu nokta ile ucgenin koseleri ve ucgenin kenarlarindaki belirli noktalar arasindaki mesafeleri iliskilendiren bir esitsizliktir Adini Amerikali bir matematikci olan dan almistir Barrow esitsizligiAciklamaP displaystyle P ABC displaystyle triangle ABC ucgeninin icinde rastgele bir nokta olsun P displaystyle P ve ABC displaystyle triangle ABC den U displaystyle U V displaystyle V ve W displaystyle W yi BPC displaystyle angle BPC CPA displaystyle angle CPA ve APB displaystyle angle APB nin aciortaylarinin sirasiyla BC displaystyle BC CA displaystyle CA AB displaystyle AB kenarlariyla kesistigi noktalar olarak tanimlayin Ardindan Barrow esitsizligi sunu belirtir PA PB PC 2 PU PV PW displaystyle PA PB PC geq 2 PU PV PW Esitlik sadece eskenar ucgen durumunda saglanir ve bu durumda P displaystyle P ucgenin merkezidir Ispatd1 PA displaystyle d 1 PA d2 PB displaystyle d 2 PB d3 PC displaystyle d 3 PC l1 PU displaystyle l 1 PU l2 PV displaystyle l 2 PV l3 PW displaystyle l 3 PW 281 BPC displaystyle 2 theta 1 angle BPC 282 CPA displaystyle 2 theta 2 angle CPA ve 283 APB displaystyle 2 theta 3 angle APB olsun Ispat edilmesi gereken ifade d1 d2 d3 2 l1 l2 l3 displaystyle d 1 d 2 d 3 geq 2 l 1 l 2 l 3 olur Asagidaki ozdeslikleri cikarmak kolaydir l1 2d2d3d2 d3cos81 displaystyle l 1 frac 2d 2 d 3 d 2 d 3 cos theta 1 l2 2d1d1d3 d1cos82 displaystyle l 2 frac 2d 1 d 1 d 3 d 1 cos theta 2 l1 2d1d2d1 d2cos83 displaystyle l 1 frac 2d 1 d 2 d 1 d 2 cos theta 3 Aritmetik Ortalama Geometrik Ortalama esitsizligi ve yukaridaki sonucla bu su anlama gelir l1 l2 l3 d2d3cos81 d3d1cos82 d1d2cos83 12 d1 d2 d3 displaystyle l 1 l 2 l 3 leq sqrt d 2 d 3 cos theta 1 sqrt d 3 d 1 cos theta 2 sqrt d 1 d 2 cos theta 3 leq frac 1 2 d 1 d 2 d 3 Istenen ifade ispatlanmis olur GenellestirmeBarrow esitsizligi disbukey cokgenlere kadar genisletilebilir Koseleri A1 A2 An displaystyle A 1 A 2 ldots A n olan disbukey bir cokgen icin P displaystyle P cokgenin icindeki rastgele bir nokta ve Q1 Q2 Qn displaystyle Q 1 Q 2 ldots Q n A1PA2 An 1PAn AnPA1 displaystyle angle A 1 PA 2 ldots angle A n 1 PA n angle A n PA 1 aciortaylari ile A1A2 An 1An AnA1 displaystyle A 1 A 2 ldots A n 1 A n A n A 1 iliskili cokgen kenarlarinin kesisimleri olsun ardindan asagidaki esitsizlik gecerlidir k 1n PAk sec pn k 1n PQk displaystyle sum k 1 n PA k geq sec left frac pi n right sum k 1 n PQ k Burada sec x displaystyle sec x sekant fonksiyonunu belirtir Ucgen durumu yani n 3 displaystyle n 3 icin sec p3 2 displaystyle sec left tfrac pi 3 right 2 oldugundan esitsizlik Barrow esitsizligine donusur TarihceBarrow Erdos Mordell esitsizligini guclendirir PA PB PC 2 PQa PQb PQc 2 PFa PFb PFc displaystyle begin aligned amp quad PA PB PC amp geq 2 PQ a PQ b PQ c amp geq 2 PF a PF b PF c end aligned Barrow esitsizligi PU displaystyle PU PV displaystyle PV ve PW displaystyle PW nin P displaystyle P noktasindan ucgenin kenarlarina olan uc uzaklik ile degistirilmesi haricinde ayni bicime sahip olan guclendirir Adini dan almistir Barrow un bu esitsizligin kaniti 1937 de kanitlayan American Mathematical Monthly dergisinde ortaya atilan bir probleme cozum olarak yayinlandi 1961 gibi erken bir tarihte Barrow esitsizligi olarak adlandirildi Daha basit bir kanit daha sonra tarafindan verildi Ayrica bakinizGeometride Euler teoremiKaynakca a b c Erdos Paul 1937 Solution to problem 3740 44 4 ss 252 254 doi 10 2307 2300713 JSTOR 2300713 M Dinca A Simple Proof of the Erdos Mordell Inequality 13 Kasim 2020 tarihinde Wayback Machine sitesinde In Articole si Note Matematice 2009 Hans Christof Lenhard Verallgemeinerung und Verscharfung der Erdos Mordellschen Ungleichung fur Polygone In Archiv fur Mathematische Logik und Grundlagenforschung Band 12 S 311 314 doi 10 1007 BF01650566 Almanca 1961 New inequalities for a triangle and an internal point cilt 53 ss 157 163 doi 10 1007 BF02417793 MR 0124774 1962 On geometric problems of Erdos and Oppenheim 46 357 ss 213 215 JSTOR 3614019 Dis baglantilarBarrow s Inequality 4 Haziran 2018 tarihinde Wayback Machine sitesinde Wolfram Demonstrations ProjectKonuyla ilgili yayinlarMalesevic Branko amp Petrovic Maja 2014 Barrow s Inequality and Signed Angle Bisectors Journal of Mathematical Inequalities 10 7153 jmi 08 40 Makale 10 Kasim 2020 tarihinde Wayback Machine sitesinde veya Makale 10 Agustos 2017 tarihinde Wayback Machine sitesinde Liu Jian 2016 Refinements of the Erdos Mordell inequality Barrow s inequality and Oppenheim s inequality Journal of Inequalities and Applications 2016 10 1186 s13660 015 0947 2 Makale Liu Jian 2019 New Refinements of the Erdos Mordell Inequality and Barrow s Inequality https doi org 10 3390 math7080726 Makale
 Azərbaycanca
Azərbaycanca Deutsch
Deutsch 日本語
日本語 Lietuvos
Lietuvos සිංහල
සිංහල Türkçe
Türkçe Українська
Українська United State
United State





