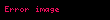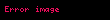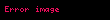Adi logaritma (On tabanlı logaritma, Genel Logaritma) taban olarak 10 un kullanıldığı bir logaritma fonksiyonudur. Logaritmada her pozitif sayı taban olarak kullanılabilir. Ama uygulamada en yaygın logaritma tabanları 10 ve e=2,718281.. dir. 10 tabanlı logaritmaya adi logaritma denilir. Fonksiyon olarak gösterilirse de, genellikle 10 indisi ihmal edilerek sadece olarak gösterilmesi de mümkündür.

Logaritma kuralları
denklemi ters fonksiyon olarak yazılırsa;
olarak gösterilir. Buna göre 10 sayısının l0 tabanına göre logaritması 1 dir.
On tabanlı logaritma da logaritmanın genel kurallarına tabidir. Yani;
Örnekler
olduğuna göre
Tablolar
Sayıların logaritmaları bilimsel hesap makinelerinde ve cep telefonlarında bulunabilir. Ayrıca, pek çok kitapla ve bilgisayar sitesinde adi logaritma tabloları vardır. Bu tablolarda okunan değer bir ondalık kesir yani 1 den küçük bir rakamdır. Bu ondalık değere mantisa denilir. Kullanıcı bu rakamın başına bir de tam sayı ekler. Bu tam sayıya da karakteristik denilir. Bu karakteristik,
- 1 ile 10 arasında (10 hariç): 0
- 10 ile 100 arasında (100 hariç): 1
- 100 ile bin arasında (1000 hariç): 2
- 1000 ile 10000 arasında (10000 hariç): 3 tür
Yani toplam basamak sayısının bir altıdır. Mesela 2000000 sayısı için beş basamaklı bir logaritma tabloda bulunan mantisa 0.30103 tür. 2000000 sayısının toplam basamak sayısı 7 dir. Bu yüzden logaritmada karakteristik te bunun bir altı yanı 6 dır. Sonuç 6.30103 tür.
Kaynakça
- ^ Arthur Graham Hall; Fred Goodrich Frink (1909). "Chapter IV. Logarithms [23] Common logarithms". Trigonometry (İngilizce). Part I: Plane Trigonometry. New York: Henry Holt and Company. s. 31.
- ^ ["Mathfun sitesi (İngilizce)". 20 Haziran 2019 tarihinde kaynağından . Erişim tarihi: 19 Temmuz 2019. Mathfun sitesi (İngilizce)] 20 Haziran 2019 tarihinde Wayback Machine sitesinde .
wikipedia, wiki, viki, vikipedia, oku, kitap, kütüphane, kütübhane, ara, ara bul, bul, herşey, ne arasanız burada,hikayeler, makale, kitaplar, öğren, wiki, bilgi, tarih, yukle, izle, telefon için, turk, türk, türkçe, turkce, nasıl yapılır, ne demek, nasıl, yapmak, yapılır, indir, ücretsiz, ücretsiz indir, bedava, bedava indir, mp3, video, mp4, 3gp, jpg, jpeg, gif, png, resim, müzik, şarkı, film, film, oyun, oyunlar, mobil, cep telefonu, telefon, android, ios, apple, samsung, iphone, xiomi, xiaomi, redmi, honor, oppo, nokia, sonya, mi, pc, web, computer, bilgisayar
Adi logaritma On tabanli logaritma Genel Logaritma taban olarak 10 un kullanildigi bir logaritma fonksiyonudur Logaritmada her pozitif sayi taban olarak kullanilabilir Ama uygulamada en yaygin logaritma tabanlari 10 ve e 2 718281 dir 10 tabanli logaritmaya adi logaritma denilir Fonksiyon log10 displaystyle log 10 olarak gosterilirse de genellikle 10 indisi ihmal edilerek sadece log displaystyle log olarak gosterilmesi de mumkundur 10 tabanli logaritma egrisi 10 un logartmasi 1 100 un logaritmasi 2 dirLogaritma kurallarim 10n displaystyle m 10 n quad denklemi ters fonksiyon olarak yazilirsa n log10 m displaystyle n log 10 m quad olarak gosterilir Buna gore 10 sayisinin l0 tabanina gore logaritmasi 1 dir On tabanli logaritma da logaritmanin genel kurallarina tabidir Yani log10 a b log10 a log10 b displaystyle log 10 a cdot b log 10 a log 10 b log10 a b log10 a log10 b displaystyle log 10 a b log 10 a log 10 b log10 a p p log10 a displaystyle log 10 a p p cdot log 10 a Ornekler105 100000 displaystyle 10 5 100000 quad olduguna gore log10 100000 5 displaystyle quad log 10 100000 5 quad log10 100 1000 log10 100 log10 1000 2 3 5 displaystyle log 10 100 cdot 1000 log 10 100 log 10 1000 2 3 5 log10 105 5 log10 10 5 1 5 displaystyle log 10 10 5 5 cdot log 10 10 5 cdot 1 5 log10 1000000 10 log10 1000000 log10 10 6 1 5 displaystyle log 10 1000000 10 log 10 1000000 log 10 10 6 1 5 TablolarSayilarin logaritmalari bilimsel hesap makinelerinde ve cep telefonlarinda bulunabilir Ayrica pek cok kitapla ve bilgisayar sitesinde adi logaritma tablolari vardir Bu tablolarda okunan deger bir ondalik kesir yani 1 den kucuk bir rakamdir Bu ondalik degere mantisa denilir Kullanici bu rakamin basina bir de tam sayi ekler Bu tam sayiya da karakteristik denilir Bu karakteristik 1 ile 10 arasinda 10 haric 0 10 ile 100 arasinda 100 haric 1 100 ile bin arasinda 1000 haric 2 1000 ile 10000 arasinda 10000 haric 3 tur Yani toplam basamak sayisinin bir altidir Mesela 2000000 sayisi icin bes basamakli bir logaritma tabloda bulunan mantisa 0 30103 tur 2000000 sayisinin toplam basamak sayisi 7 dir Bu yuzden logaritmada karakteristik te bunun bir alti yani 6 dir Sonuc 6 30103 tur log10 2000000 6 30103 displaystyle log 10 2000000 6 30103 Kaynakca Arthur Graham Hall Fred Goodrich Frink 1909 Chapter IV Logarithms 23 Common logarithms Trigonometry Ingilizce Part I Plane Trigonometry New York Henry Holt and Company s 31 Mathfun sitesi Ingilizce 20 Haziran 2019 tarihinde kaynagindan Erisim tarihi 19 Temmuz 2019 Mathfun sitesi Ingilizce 20 Haziran 2019 tarihinde Wayback Machine sitesinde
 Azərbaycanca
Azərbaycanca Deutsch
Deutsch 日本語
日本語 Lietuvos
Lietuvos සිංහල
සිංහල Türkçe
Türkçe Українська
Українська United State
United State